dùng thước và compa để chia góc vuông cho trước thành 3 góc có số đo bằng nhau

Những câu hỏi liên quan
Chia một góc vuông thành 3 góc bằng nhau bằng thước kẻ và compa.
Việc chia ba một góc thì sao? Tại sao nó lại khó? Có một số trường hợp tam giác đặc biệt có thể làm được, ví dụ như góc π/2 (90 độ). Đối với trường hợp tổng quát, người Hy Lạp vẫn không thể nghĩ ra được cách làm mặc nhiều đã mất rất nhiều công sức để giải quyết vấn đề này.
| Chia ba một góc bằng thước kẻ có đánh dấu |
Chia ba một góc tùy ý có thể thực hiện được nếu như bạn "ăn gian" bằng cách sử dụng thước đo thay vì một cạnh thẳng đơn giản (bạn có thể tiềm hiểu cách làm trong trang hỏi đáp sci.math), hoặc ngay cả khi bạn chỉ cần vẽ hai điểm nhỏ trên cạnh thẳng của bạn. Tuy nhiên để "chơi đúng luật", bạn không được để bất kì dấu vết nào trên cạnh thẳng - nó phải hoàn toàn trống.
Vấn đề liệu việc chia góc làm ba phần bằng nhau có thể được thực hiện trong trường hợp tổng quát hay không vẫn là một bí ẩn toán học trong hàng thiên niên kỉ - vào năm 1837 điều đó được chứng minh là không thể bởi Pierre Wantzel, một nhà toán học người Pháp và chuyên gia về số học. Đây là một thành tựu tuyệt vời đôi với một người đàn ông 23 tuổi, người mà sau đó qua đời khi còn rất trẻ ở tuổi 33.
Vậy tại sao lại không thể? Pierre cho thấy rằng hai vấn đề chia một góc làm ba phần bằng nhau và giải quyết một phương trình bậc ba là như nhau. Hơn nữa, ông cho thấy rằng chỉ có một số ít phương trình bậc ba có thể giải quyết được bằng phương pháp cạnh thẳng - com-pa, hầu hết đều không thể. Do đó ông đã suy luận rằng hầu hết các góc đều không thể chia làm ba được.
Tuy nhiên, việc chia ba một góc một cách gần đúng được mô tả bởi Steinhaus trong cuốn Mathematical Snapshots, 3rd ed. New York: Dover, 1999. (trước đó nó được môt tả bởi Wazewski 1945; và Peterson, G. "Approximation to an Angle Trisection." Two-Year Coll. Math. J. 14, 166-167, 1983.).
Đúng 0
Bình luận (0)
a) Em hãy dùng compa kiểm tra xem tam giác nào dưới đây (Hình 4) có 3 cạnh bằng nhau.
b) Với hình tìm được, dùng thước đo góc để kiểm tra các góc của tam giác đó có bằng nhau không?
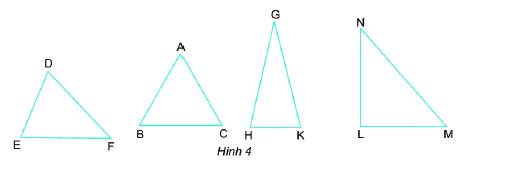
a) Chỉ có ABC là hình có 3 cạnh bằng nhau.
b) Các góc của tam giác ABC bằng nhau và đều bằng \(60^\circ \) .
Đúng 1
Bình luận (0)
hãy chia một góc bất kỳ thành 3 phần bằng nhau bằng thước kẻ và compa
Chia một góc thành nhiều phần bằng nhau bằng thước thẳng và compa
* * *
Kết quả nghiên cứu nầy gồm 3 phần:
Phần 1 – Chia ba một góc cho sẵn bằng thước thẳng và compa
Phần 2 – Vẽ một đa giác đều có n cạnh bằng thước thẳng và compa
Phần 3 – Chia một góc thành nhiều phần bằng nhau.
Hệ luận Thuận Hoà (hay Thuanhoa’s corollary)
____________________
Phần 1 – Chia ba một góc cho sẵn bằng thước thẳng
và compa
(Phần này là tiền đề cho Phần 3. Thuận Hoà chỉ trình bày lại những kết quả đã biết và phổ biến trong nhiều sách và Internet.)
“Chia một góc cho sẵn thành 3 phần bằng nhau” là một trong 3 bài toán trong hình học phẳng Euclide “không giải được” từ thời các nhà toán học cổ Hy lạp. Thật ra, phải nói rõ ra là “không vẽ được bằng compa và thước thẳng không chia độ” mới đúng. Thước thẳng không chia độ là thước chỉ dùng để gạch đường thẳng nối 2 điểm hay qua một điểm và thẳng góc với một đường thẳng khác mà thôi. Hai bài toán khác là: (i) Vẽ một hình vuông có diện tích bằng diện tích của một vòng tròn cho sẵn và (ii) Vẽ một hình lập phương có thể tích gắp đôi thể tích của một hình lập phương cho sẵn.
Thật ra, không phải tất cả mọi góc đều không thể chia 3 đuợc bằng phép vẽ chỉ dùng compas và thước thẳng.
Ta biết rằng 1/3 của góc 60o là 20o, nhưng chia một góc 60o làm 3 phần không thể thực hiện được chỉ bằng compa và thước thẳng. Lý do là vì chia một góc 60o làm 3 phần tương đương với giải một phương trình bậc 3 có nghiệm số không hửu tỉ. Điều đó có thể thấy được qua một hệ thức lượng giác là cos(3θ) = 4cos3(θ) − 3cos(θ).
Nếu 3θ = 60o thì cos(3θ) = 1/2. Chia góc 3θ = 60o làm 3 phần tương đương với tìm một góc θ thoả phương trình:
4cos3(θ) − 3cos(θ) = 1/2
hay 8x3 – 6x – 1 = 0 nếu đặt x = cos(θ)
hay, đặt y = 2x
y3 – 3y – 1 = 0 (1)
Phương trình (1) không có nghiệm hửu tỉ. Thật vậy, nếu (1) có một nghiệm hửu tỉ r/s với r và s là 2 số nguyên không có thừa số chung, thì thay y = r/s vào (1) và rút gọn:
= > s3 = r(r2 -3s2) chia đúng cho r => s và r có thừa số chung. trừ khi r = ± 1.
= > r3 = s2(s + 3r) chia đúng co s2 => s và r có thừa số chung, trừ khi s = ± 1.
Vì r và s được giả thiết là không có thừa số chung, nên trường hợp nầy chỉ chấp nhận được khi
r = ± 1 và s = ± 1 và nghiệm số hửu tỉ của phương trình (1) chỉ có thể là +1 hay -1. Mà cà +1 và -1 dều không nghiệm đúng (1).
Tóm lại: phương trình (1) không có nghiệm hửu tỉ. Điều đó chứng tỏ rằng không vẽ được một góc 20o từ một góc 60o cho sẵn bằng compa và thước thẳng.
Chia ba một góc cho sẵn thường không thhể được với compa và thước thẳng. Thước thẳng nầy chỉ có nhiệm vụ duy nhất là để kẻ đường thẳng mà thôi.
Tuy nhiên, với một thước thẳng có chia độ, được hiểu là thước có thể dùng để đo khoảng cách của 2 điểm, thì bài toán chia ba một góc cho sẵn có thể giải được như dưới đây.
Ta có: BA = BC = CD
=> Hai tam giác BAC và BCD cân lần lượt ở B và C.
Gọi b là 2 góc đáy của tam giác BCD và c là 2 góc đáy của tam giác BAC.
=> Góc CBD = CDB = b và Góc BCA = BAC = c
=> Góc BCA = CBD + CDB => c = 2b (Góc ngoài tam giác)
Gọi d là góc ở đỉnh của tam giác cân BAC
=> Góc ABC = d = 180o – 2c = 180o – 4b vì c = 2b
Tổng số các góc ở đỉnh B bằng 180o:
= > a + d + b = 180o
= > a + (180o – 4b) + b = 180o => b = a/3
Như vậy là ta đã vẽ được một góc bằng 1/3 một góc cho sẵn.
Đúng 0
Bình luận (0)
Dựng 1 tia có đầu mút là 1 đầu bất kì của đoạn thẳng đã cho.
Dùng compa xác định 3 đoạn thẳng bằng nhau liên tiếp trên tia vừa vẽ, bắt đầu từ điểm gốc của tia.
Nối điểm cuối của đoạn thẳng cuối với điểm còn lại của đoạn thẳng đã cho.
Dựng các đường thẳng đi qua các điểm đã xác định trên tia và song song với đoạn thẳng vừa mới dựng 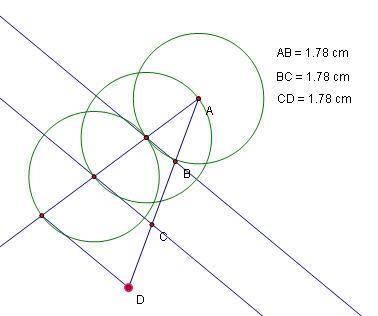
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
1) Cho tam iacs ABC , hai đg cao BD,CE cắt nhau tại H cho biết ACBH . C/m tam giác ABC có góc B 45 độ hoặc 135 độ2)dùng thước và compa để chia góc vuông cho trước thành 3 phần nhau 3)Cho tam giác ABC vuông cân tại A , qua A vê đg thẳng d thay đổi , ve BD và CE cùng vuông góc d (DE thuộ d). Cmr BD^2+CE^2 ko đổi4) Cho tam giác ABC có AB1 , góc A 75 độ , góc B 60 độ . Trên mửa mp BC có chứa A ve tia Bz sao cho góc CBz 15 độ a)C/m DC vuông góc BC b)Tính tổng BC^2+CD^25) Tam giác ABC vuông c...
Đọc tiếp
1) Cho tam iacs ABC , hai đg cao BD,CE cắt nhau tại H cho biết AC=BH . C/m tam giác ABC có góc B =45 độ hoặc 135 độ
2)dùng thước và compa để chia góc vuông cho trước thành 3 phần = nhau
3)Cho tam giác ABC vuông cân tại A , qua A vê đg thẳng d thay đổi , ve BD và CE cùng vuông góc d (DE thuộ d). Cmr BD^2+CE^2 ko đổi
4) Cho tam giác ABC có AB=1 , góc A =75 độ , góc B =60 độ . Trên mửa mp BC có chứa A ve tia Bz sao cho góc CBz =15 độ
a)C/m DC vuông góc BC
b)Tính tổng BC^2+CD^2
5) Tam giác ABC vuông cân tại A , trung tuyến AM (M tđ BC) . Cmr AE=CF
Xét 2 tam giác AEC và tam giác HEB có:
\(\widehat{AEC}=\widehat{HEB}\left(=90^o\right)\)
AC=BH (giả thiết)
\(\widehat{CAE}=\widehat{BHE}\left(=\widehat{DHC}\right)\)
\(\Rightarrow\Delta AEC=\Delta HEB\left(ch.gn\right)\)
=> EC=EB (2 cạnh tương ứng)
=> tam giác ECB cân tại E
=> \(\widehat{B}=45^o\)
Đây chỉ là TH góc B nhọn, còn TH góc B tù thì làm tương tự tìm ra góc B=135 độ
Đúng 0
Bình luận (0)
Lấy B thuộc Ox , A thuộc Oy sao cho OA=OB
Dùng compa vẽ đtron (O;OB) và (B;OB), 2 đường tròn cắt nhau tại D ,nối O với D
Dùng compa vẽ đtron (D;R) và (B;R) (với R là bán kính bất kì), 2 đtron cắt nhau tại H, nối O với H
OD và OH chia góc ra làm 3 phần bằng nhau
Đúng 0
Bình luận (0)
\(\widehat{BAD}=\alpha\Rightarrow\widehat{CAE}=90^o-\alpha\)
Ta có: Tam giác ABC vuông cân tại A => AB=AC
\(BD^2=\left(sin\left(\alpha\right).AB\right)^2=sin^2\alpha.AB^2\)
\(CE^2=\left(sin\left(90^o-\alpha\right).AC\right)^2=\left(cos\alpha.AC\right)^2=cos^2\alpha.AC^2\)
\(\Rightarrow BD^2+CE^2=sin^2\alpha.AB^2+cos^2a.AC^2=sin^2\alpha.AB^2+cos^2\alpha.AB^2=AB^2\left(sin^2\alpha+cos^2\alpha\right)=AB^2\)
Do AB không đổi nên BD2+CE2 không đổi (đpcm)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
a) Cho 6 tam giác đều có cùng độ dài cạnh. Hãy ghép 6 tam giác đều thành một hình (Hình 6).
b) Dùng compa và thước đo góc đo các cạnh và góc của hình vừa nhận được. Cho ý kiến nhận xét.
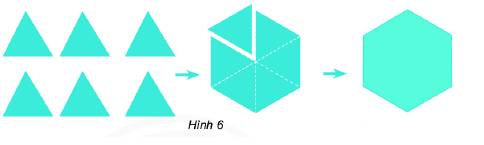
a) Ghép 6 tam giác đều thành hình mới.
b) Hình vừa nhận được có các góc bằng nhau, các cạnh bằng nhau.
Đây là hình lục giác đều.
Đúng 0
Bình luận (0)
mọi người giúp mình cách để chia 1 góc nhọn thành các phần bằng nhau chỉ bằng với thước kẻ và compa nha
giúp mình với
nhưng chia ra làm bao nhiêu phần mới được chứ?
Đúng 0
Bình luận (0)
chia thành 2,3,4,5,6 phần bằng nhau
Đúng 0
Bình luận (0)
Quan sát hình chữ nhật ở hình 4.8a.1. Nêu tên đỉnh, cạnh, đường chéo, hai cạnh đối của hình chữ nhật ABCD (h.4.8b).2. Dùng thước đo góc để đo và so sánh các góc của hình chữ nhật ABCD.3. Dùng thước thẳng hoặc compa để so sánh hai cạnh đối, hai đường chéo của hình chữ nhật ABCD.
Đọc tiếp
Quan sát hình chữ nhật ở hình 4.8a.
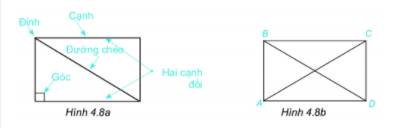
1. Nêu tên đỉnh, cạnh, đường chéo, hai cạnh đối của hình chữ nhật ABCD (h.4.8b).
2. Dùng thước đo góc để đo và so sánh các góc của hình chữ nhật ABCD.
3. Dùng thước thẳng hoặc compa để so sánh hai cạnh đối, hai đường chéo của hình chữ nhật ABCD.
1) Đỉnh: A, B, C, D
Cạnh: AB, BC, CD, DA
Đường chéo: AC, BD
Hai cạnh đối: AB và CD; BC và AD
2) Ta đo được: \(\widehat{A} = 90^0; \widehat{B} = 90^0; \widehat{C} = 90^0; \widehat{D} = 90^0\). Vậy các góc của hình chữ nhật đều bằng nhau và bằng 90o
3) Ta đo được: AB = CD ; AD = BC nên hai cạnh đối của hình chữ nhật bằng nhau
AC = BD nên hai đường chéo của hình chữ nhật bằng nhau.
Đúng 1
Bình luận (0)
a) Dùng thước đo góc để đo các góc của hình tứ giác MNPQ
b) Nêu tên các cặp góc có số đo bằng nhau của hình tứ giác MNPQ
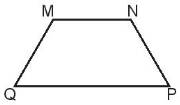
a) Góc đỉnh M, cạnh MN, MQ có số đo là 115o
Góc đỉnh N, cạnh NM, NP có số đo là 115o
Góc đỉnh Q, cạnh QM, QP có số đo là 65o
Góc đỉnh P, cạnh PN, PQ có số đo là 65o
b) Tên các cặp góc có số đo bằng nhau của hình tứ giác MNPQ là:
- Góc đỉnh M, cạnh MN, MQ và góc đỉnh N, cạnh NM, NP
- Góc đỉnh Q, cạnh QM, QP và góc đỉnh P, cạnh PN, PQ
Đúng 1
Bình luận (0)
Xem hình 21. Ước lượng bằng mắt xem góc nào vuông, nhọn tù, bẹt.
Dùng góc vuông của eke để kiểm tra lại kết quả. Dùng thước đo góc tìm số đo mỗi góc.
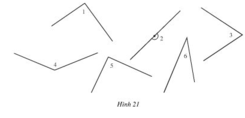
Ước lượng bằng mắt:
- Góc vuông: góc 1, góc 5
- Góc nhọn: góc 3, góc 6
- Góc tù: góc 4
- Góc bẹt: góc 2
Kết quả đo:
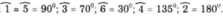
Đúng 0
Bình luận (0)





















