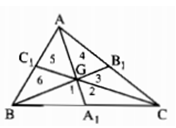
Chứng minh rằng 3 đường trung tuyến của tam giác chia tam giác thành 6 phần có diện tích bằng nhau.

Những câu hỏi liên quan
Chứng minh rằng các đường trung tuyến của tam giác chia tam giác thành 6 phần có diện tích bằng nhau
Cho tam giác ABC. Vẽ các đường trung tuyến. Chứng minh rằng các đường trung tuyến chia tam giác thành 6 phần có diện tích bằng nhau
chứng minh rằng các đường trung tuyến của một tam giác phân chia tam giác đó thành 6 tam giác mà diện tích của chúng ( đôi một ) bằng nhau
Các đường trung tuyến cắt nhau tại trọng tâm
=> vẽ hình ra sẽ nhận thấy 6 tam giác: Tam giác ABC trọng tâm G
Xét 2 tam giác có đáy chung cạnh thì hiển nhiên diện tích bằng nhau do có chung đương cao và đáy bằng nhau => diện tích bằng 1/2 diện tích tam giác đỉnh G đáy là canh tam giác ABC
Xét các tam giác đỉnh G đáy là cạnh của tam giác ABC có 3 tam giác đó có diện tích bằng nhau
Từ 2 điều trên => diện tích 6 tam giác nhỏ đó = nhau
Đúng 0
Bình luận (0)
Chứng minh rằng ba trung tuyến của một tam giác chia tam giác đó thành 6 hình tam giác có diện tích bằng nhau
GIÚP VỚI
giải chi tiết nha
Gọi AM, BN, CL là các trung tuyến của tam giác ABC => G là trọng tâm của tam giác ABC. Ta cần phải chứng minh S(GAB)=S(GBC)=S(GAC). + Hai tam giác AMC và tam giác ABC có chung đường cao hạ từ A xuống BC nên S(AMC)/S(ABC)=MC/BC=1/2 => S(AMC)=S(ABC)/2 (1) + Hai tam giác GAC và tam giác AMC có chung đường cao hạ từ C xuống AM nên S(GAC)/S(AMC)=AG/AM=2/3 (3 đường trung tuyến cắt nhau tại 1/3 mmỗi đường kể từ đáy) => S(GAC)=2.S(AMC)/3 (2) Từ (1) và (2) => S(GAC)=S(ABC)/3 + Tương tự cũng c/m được S(GAB)=S(GBC)=S(ABC)/3 => Trọng tâm của tam giác khi nối với đỉnh của tam giác ABC thì chia tam giác ABC thành 3 tam giác nhỏ có diện tích bằng nhau
Đúng 1
Bình luận (2)
Chứng minh rằng các trung tuyến của một tam giác phân chia tam giác đó thành 6 tam giác mà diện tích của chúng (đôi một) bằng nhau.
Xét sáu tam giác được đánh số là: 1, 2, 3, 4, 5, 6
Chứng minh hoàn toàn tương tự như bài 4.4 ta có
SGAB = SGBC = SGCA = 1/3 SABC
Ta lại có S1 = S2, S3 = S4, S5 = S6 (vì mỗi cặp tam giác có chung đường cao và hai đáy bằng nhau, vậy sáu tam giác 1, 2, 3, 4, 5, 6 có diện tích bằng nhau)
Đúng 0
Bình luận (0)
Chứng minh rằng các trung tuyến của một tam giác phân chia tam giác đó thành 6 tam giác mà diện tích của chúng (đôi một) bằng nhau.
Hình vẽ:
Xét sáu tam giác được đánh số là: 1, 2, 3, 4, 5, 6
Vì G là trọng tâm nên ta có:
\(S_{GAB}=S_{GBC}=S_{GCA}=\dfrac{1}{3}S_{ABC}\)
Ta lại có \(S_1=S_2;S_3=S_4;S_5=S_6\) (vì mỗi cặp tam giác có chung đường cao và hai đáy bằng nhau, vậy sáu tam giác 1, 2, 3, 4, 5, 6 có diện tích bằng nhau)
Đúng 0
Bình luận (0)
Cho tam giác ABC có đường cao AH và trung tuyến AM chia góc A thành 3 phần bằng nhau. Chứng minh rằng: Tam giác ABC là tam giác vuông và tam giác ABM là tam giác đều.
Xét ΔABM có AHvừa là đường cao, vừa là phân giác
nên ΔABM cân tại A
=>H là trung điểm của BM
Xét ΔAHC có AM là phân giác
nên AH/AC=CM/MH=CM/2MB=CM/2MC=1/2
Xet ΔAHC vuông tại H có sin ACH=AH/AC=1/2
nên góc ACH=30 độ
=>góc HAC=60 độ
=>góc BAH=1/2*góc HAC=30 độ
=>góc BAC=90 độ
=>ΔABC vuông tại A
Xét ΔABC vuông tại A có góc B+góc C=90 độ
=>góc B=60 độ
mà ΔAMB cân tại A
nên ΔAMB đều
Đúng 0
Bình luận (0)
Xét ΔABM có AHvừa là đường cao, vừa là phân giác
nên ΔABM cân tại A
=>H là trung điểm của BM
Xét ΔAHC có AM là phân giác
nên AH/AC=CM/MH=CM/2MB=CM/2MC=1/2
Xet ΔAHC vuông tại H có sin ACH=AH/AC=1/2
nên góc ACH=30 độ
=>góc HAC=60 độ
=>góc BAH=1/2*góc HAC=30 độ
=>góc BAC=90 độ
=>ΔABC vuông tại A
Xét ΔABC vuông tại A có góc B+góc C=90 độ
=>góc B=60 độ
mà ΔAMB cân tại A
nên ΔAMB đều
Đúng 0
Bình luận (0)
CMR: Ba trung tuyến của một tam giác chia tam giác đó thành 6 phần có diện tích bằng nhau:
Vẽ 1 hình tam giác đều có 3 đường trung tuyến nối từ đỉnh A,B,C đến lần lượt các điểm N,L,D sau đó tam giác được chia thành sáu phần
Vì đường trung tuyến luôn chia nửa hình tam giác thành 2 phần bằng nhau.
=> TH1: Đỉnh A: 1+6+5=2+3+4
TH2: Đỉnh B: 6+1+2=5+4+3
TH3: Đỉnh C: 1+2+3=4+5+6
====>1=6=2
5=4=3
6=5=4
1=2=3
1=6=5
2=3=4
=>> tất cả đều bằng nhau
Đúng 0
Bình luận (0)
chứng minh rằng các trung tuyến của một tam giác phân chia tam giác đó thành 6 tam giác mà diện tích của chúng( đôi một ) bằng nhau
MÌNH CẦN GẤP LẮM NHA CÁC BẠN