Question

Chứng minh rằng 3 đường trung tuyến của tam giác chia tam giác thành 6 phần có diện tích bằng nhau.

Answer 1

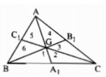
Gọi AM, BN, CL là các trung tuyến của tam giác ABC 
=> G là trọng tâm của tam giác ABC. Ta cần phải chứng minh S(GAB)=S(GBC)=S(GAC). 
+ Hai tam giác AMC và tam giác ABC có chung đường cao hạ từ A xuống BC nên 
S(AMC)/S(ABC)=MC/BC=1/2 => S(AMC)=S(ABC)/2 (1) 
+ Hai tam giác GAC và tam giác AMC có chung đường cao hạ từ C xuống AM nên 
S(GAC)/S(AMC)=AG/AM=2/3 (3 đường trung tuyến cắt nhau tại 1/3 mmỗi đường kể từ đáy) 
=> S(GAC)=2.S(AMC)/3 (2) 
Từ (1) và (2) => S(GAC)=S(ABC)/3 
+ Tương tự cũng c/m được 
S(GAB)=S(GBC)=S(ABC)/3 
=> Trọng tâm của tam giác khi nối với đỉnh của tam giác ABC thì chia tam giác ABC thành 3 tam giác nhỏ có diện tích bằng nhau

Answer 2

Bạn đặt tên cho các đỉnh rồi chứng minh các tam giác đó bằng nhau nha

Answer 3

bạn có thể áp dụng bài này 

ấn vào dòng chữ xanh 

Cmr trọng tâm chia tam giác thành 3 tam giác nhỏ có diện tích bằng nhau? | Yahoo Hỏi & Đáp

Answer 4

đơn giản như ăn cơm sườn

các tg con có đuong cao = nhau,canh day = nhau = 1/6 S_abc

_{( vi trg tuyen chia doi các canh)}

Answer 5

Nguyễn Thiện Nhân copy lộn đề rồi

Answer 6

Nguyễn Thiện Nhân mới hoàn thành 3/4 bài giải thôi nhưng cũng đủ để mình hiểu.

Answer 7

Bạn search google BDHS 6 trên youtube của hocmai.vn để biết rõ hơn về chuyên đề này nhé