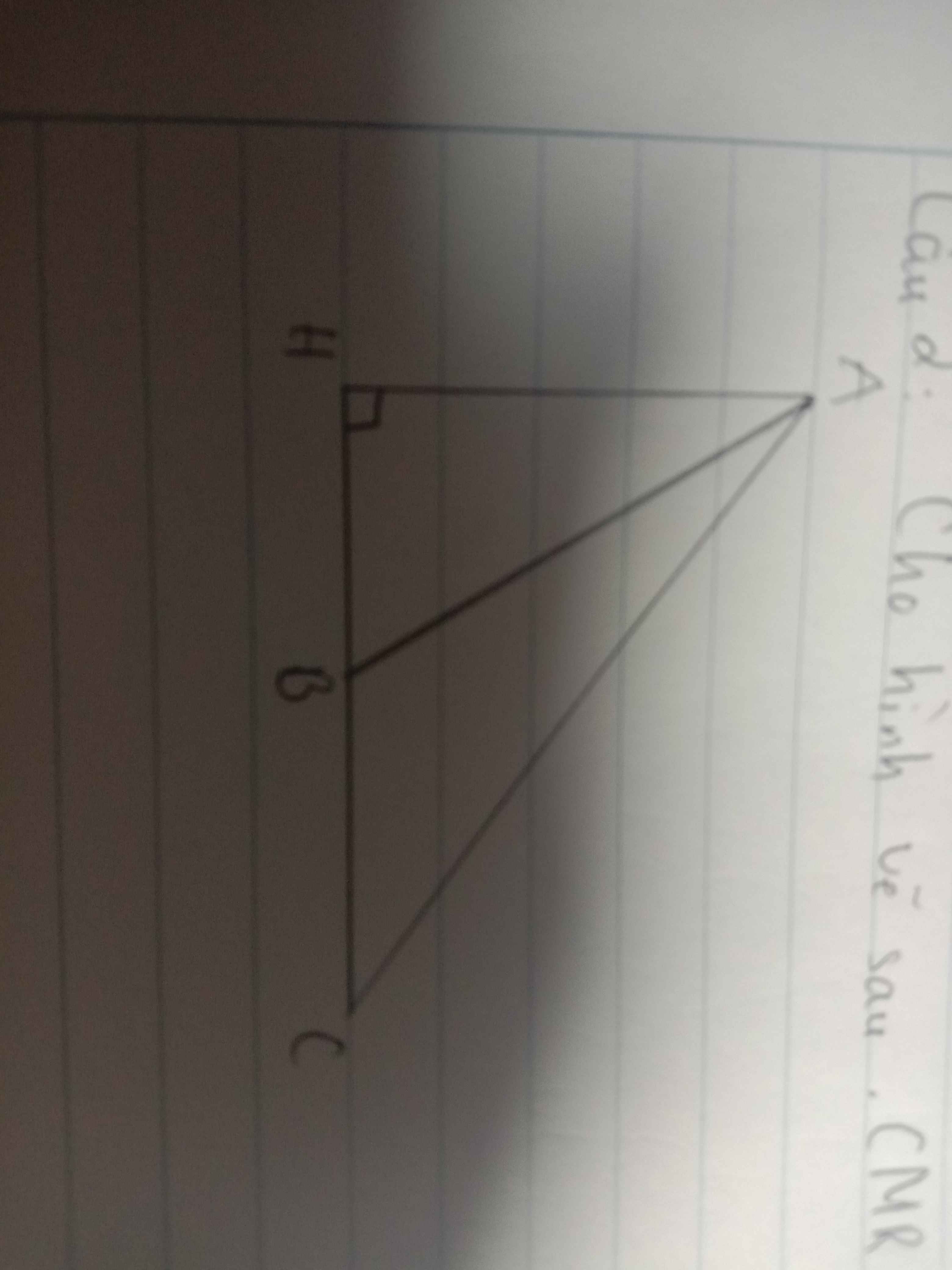
 Cho hình vẽ sau. Chứng minh rằng AH<AB<AC
Cho hình vẽ sau. Chứng minh rằng AH<AB<AC

Những câu hỏi liên quan
Cho ∆ABC biết rằng AB=9cm,AC=12cm,BC=15cm AH là đường cao a) Chứng minh ∆ABC vuông b) Tính AH,BH c)Vẽ HE vuông góc AB tại E Vẽ HI vuông góc AC tại I Chứng minh AE.AB=AI.AC VẼ HÌNH DÙM MÌNH Ạ
cho tam giác abc vuông góc ac (M thuộc AB) vẽ EMH vuông góc với BC (thuộc BC)
a) vẽ hình
b) Chứng minh rằng (M là đường trung trực của AH)
c) chứng minh rằng AMC bằng tam giác ABC
Bài 4: Cho tam giác ABC. Vẽ đường cao AH. Gọi D, E theo thứ tự là trung điểm của các cạnh AB và AC. Vẽ DI và EK cùng vuông góc với BC. Chứng minh rằng :DI = EK. Gợi ý : - Học sinh tự vẽ hình minh họa. - dựa vào đường trung bình chứng minh DI = 1/2 AH và EK = 1/2AH.
cho ΔABC vuông tại A . Vẽ đường cao AH .Trên cạnh BC lấy điểm D sao cho BD=BA
a) chứng minh rằng :Tia AC là tia phân giác của HAC
b) Vẽ DK ⊥ AC (K ∈ AC).chứng minh rằng : AK=AH
c)chứng minh rằng :AB+AC<BC+AH
a) Sửa đề: Tia AD là tia phân giác của góc HAC
Xét ΔBAD có BA=BD(gt)
nên ΔBAD cân tại B(Định nghĩa tam giác cân)
Ta có: \(\widehat{BAD}+\widehat{CAD}=90^0\)
\(\widehat{HAD}+\widehat{BDA}=90^0\)
mà \(\widehat{BAD}=\widehat{BDA}\)(ΔBAD cân tại B)
nên \(\widehat{CAD}=\widehat{HAD}\)
hay AD là tia phân giác của \(\widehat{HAC}\)(đpcm)
b) Xét ΔAKD vuông tại K và ΔAHD vuông tại H có
AD chung
\(\widehat{KAD}=\widehat{HAD}\)(AD là tia phân giác của \(\widehat{KAH}\))
Do đó: ΔAKD=ΔAHD(cạnh huyền-góc nhọn)
Suy ra: AK=AH(hai cạnh tương ứng)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A ( AC ), đường cao AH. Vẽ hình vuông AHIk (điểm H nằm giữa hai điểm C và I), hai đường thẳng KI và AB cắt nhau tại D
a)Chứng minh rằng AD = AC
b)Vẽ hình bình hành ADEC có hai đường chéo cắt nhau tại O, chứng minh rằng ba điểm O,H,K cùng nằm trên đường trung trực của đoạn AI và tứ giác KOEI là hình thang.
c)Cho AH = 8. Tính AI
Cho tam giác ABC vuông tại A ( AC ), đường cao AH. Vẽ hình vuông AHIk (điểm H nằm giữa hai điểm C và I), hai đường thẳng KI và AB cắt nhau tại D
a)Chứng minh rằng AD = AC
b)Vẽ hình bình hành ADEC có hai đường chéo cắt nhau tại O, chứng minh rằng ba điểm O,H,K cùng nằm trên đường trung trực của đoạn AI và tứ giác KOEI là hình thang.
c)Cho AH = 8. Tính AI
giúp em với
Cho tam giác ABC vuông tại A, AC = 2AB, đường cao AH. Gọi D là điểm đối xứng với H qua A. Vẽ hình chữ nhật CHDE
a) Gọi I là trung điểm của AC, K là hình chiếu của I trên BC. Chứng minh rằng CK = AH
b) Chứng minh rằng CHDE là hình vuông
Cho ABC cân tại A . Vẽ BH ⊥ AC ( H AC), CK ⊥ AB, ( K AB ). a/ Vẽ hình b/ Chứng minh rằng AH = AK c/ Gọi I là giao điểm BH và CK. Chứng minh 𝐾𝐴𝐼 ̂ = 𝐻𝐴𝐼 ̂ d/ Đường thẳng AI cắt BC tại P. Chứng minh AI ⊥ BC tại P.









