cho tam giác ABC. Gọi M,N là hai điểm lần lượt chạy trên AB và AC sao cho AM/AB+AN/AC=1. Chứng minh rằng chung điểm I của MN chạy trên một mặt phẳng cố định.

Những câu hỏi liên quan
Cho tam giác cân ABC . M và N là hai điểm chuyển động trên hai cạnh AB , AC sao cho AC =CN . Chứng minh rằng trung điểm I của đoạn MN chạy trên một đoạn thẳng cố định
Cho tam giác ABC cân tại A. TRên các cạnh AB ; AC lần lượt lấy các điểm M và N sao cho AM + AN = AB. CHứng minh rằng: Khi M và N di chuyển trên AB và AC nhưng vẫn thỏa mãn AM + AN = AB thì đường trung trực của MN luôn đi qua một điểm cố định
cho tam giác ABC, trên tia đối tia AB lấy điểm M sao cho AB=AM. Trên tia AC lấy điểm N sao cho AC=AN. Chứng minh:
a) tam giác ABC=tam giác AMN
b) chứng minh BC//MN
c) gọi P và Q lần lượt là trung điểm của BC và MN. Chứng minh A là trung điểm của PQ
Cho tam giác ABC có AB AC. Trên các cạnh AB và AC lần lượt lấy các điểm M và N thay đổi sao cho BM CN. Gọi K là trung điểm MC, kẻ đường thẳng đi qua trung điểm J của Bc và trung điểm I của MN cắt các đường thẳng AB và AC lần lượt ở D và Ea) CMR : Tam giác IJK và tam giác ADE cânb) Chứng minh trung điểm I của MN luôn nằm trên một tia cố địnhc) Chứng minh rằng trung trực của MN luôn đi qua một điểm cố định
Đọc tiếp
Cho tam giác ABC có AB < AC. Trên các cạnh AB và AC lần lượt lấy các điểm M và N thay đổi sao cho BM = CN. Gọi K là trung điểm MC, kẻ đường thẳng đi qua trung điểm J của Bc và trung điểm I của MN cắt các đường thẳng AB và AC lần lượt ở D và E
a) CMR : Tam giác IJK và tam giác ADE cân
b) Chứng minh trung điểm I của MN luôn nằm trên một tia cố định
c) Chứng minh rằng trung trực của MN luôn đi qua một điểm cố định
a/ Xét tam giác MNC có:
I trung điểm MN
K trung điểm MC
Vậy IK là đường trung bình của tam giác MNC
=> IK = 1/2 NC (1)
Mặt khác, xét tam giác MCB có:
K trung điểm MC
J trung điểm BC
Vậy KJ là đường trung bình tam giác MCB
=> KJ =1/2 BM (2)
mà BM = CN (gt) (3)
Từ (1), (2) và (3) => IK = KJ
=> Tam giác IKJ cân tại K
Lại có IK // NC (tính chất đường trung bình trong tam giác)
=> góc KIJ = góc CEJ (đồng vị) (4)
KJ // BM (tính chất đường trung bình trong tam giác)
=> góc KJI = ADJ (so le trong) (5)
mà góc KIJ = góc KJI (tam giác IKJ cân tại K) (6)
Từ (4), (5), (6) => góc ADE = góc AED
=> Tam giác ADE cân tại A (đpcm)
b/ Ko biết làm ^^
c/ Ko biết làm ^^
Đúng 0
Bình luận (0)
Cho hai tia Ax và By vuông góc với nhau nhận AB làm đoạn vuông góc chung. Gọi M và N là hai điểm di động lần lượt trên Ax và By sao cho AM + BN MN.Đặt AB 2a, gọi O là trung điểm của AB và H là hình chiếu vuông góc điểm O trên đường thẳng MNa) Chứng minh rằng OH a, HM AN, HN BN.b) Gọi Bx là tia song song và cùng chiều với tia Ax và K là hình chiếu vuông góc của H trên mặt phẳng (Bx; By). Chứng minh BK là phân giác của góc ∠xBy.C. Chứng minh điểm H nằm trên một đường tròn cố định.
Đọc tiếp
Cho hai tia Ax và By vuông góc với nhau nhận AB làm đoạn vuông góc chung. Gọi M và N là hai điểm di động lần lượt trên Ax và By sao cho AM + BN = MN.
Đặt AB = 2a, gọi O là trung điểm của AB và H là hình chiếu vuông góc điểm O trên đường thẳng MN
a) Chứng minh rằng OH = a, HM = AN, HN = BN.
b) Gọi Bx' là tia song song và cùng chiều với tia Ax và K là hình chiếu vuông góc của H trên mặt phẳng (Bx'; By). Chứng minh BK là phân giác của góc ∠x'By.
C. Chứng minh điểm H nằm trên một đường tròn cố định.
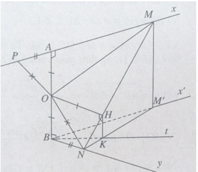
Theo giả thiết ta có M và N là hai điểm di động lần lượt trên hai tia Ax và By sao cho AM + BN = MN.
a) Kéo dài MA một đoạn AP = BN, ta có MP = MN và OP = ON.
Do đó ΔOMP = ΔOMN (c.c.c)
⇒ OA = OH nên OH = a.
Ta suy ra HM = AM và HN = BN.
b) Gọi M’ là hình chiếu vuông góc của điểm M trên mặt phẳng (Bx’, By) ta có:
HK // MM’ với K ∈ NM’.
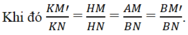
Do đó đối với tam giác BNM’ đường thẳng BK là phân giác của góc (x'By) .
c) Gọi (β) là mặt phẳng (AB, BK). Vì HK // AB nên HK nằm trong mặt phẳng (β) và do đó H thuộc mặt phẳng (β). Trong mặt phẳng (β) ta có OH = a. Vậy điểm H luôn luôn nằm trên đường tròn cố định, đường kính AB và nằm trong mặt phẳng cố định (β) = (AB, BK)
Đúng 0
Bình luận (0)
Cho tam giác abc cân tại a. m và n là 2 điểm chuyển động trên 2 cạnh ab, ac sao cho am=cn. CMR trung điểm i của mn chạy trên một đoạn thẳng cố định
Cho tam giác ABC cân tại A. Lấy điểm M trên cạnh AB, điểm N trên cạnh AC sao cho AM = CN. Gọi I là trung điểm của MN. Đường thẳng qua I song song với BC cắt AB, AC lần lượt tai D, E. Chứng minh rằng DE là đường trung bình của tam giác ABC.
Cho tam giác ABC, gọi các điểm M, N lần lượt nằm trên các cạnh AB, AC sao cho : AB = 3 x AM, AC = 3 x AN. Gọi I là điểm chính giữa của cạnh BC.
a) Chứng tỏ rằng tứ giác BMNC là hình thang và BC = 3 x MN.
b) Chứng tỏ rằng các đoạn thẳng BN, CM, AI cùng cắt nhau tại một điểm.
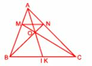
a) Vì AB = 3 x AM, AC = 3 x AN, nên MB = 2/3 x AB, NC = 2/3 x AC.
Từ đó suy ra : dt (MBC) = 2/3 x dt (ABC) (chung chiều cao từ C
dt (NCB) = 2/3 x dt (ABC) (chung chiều cao từ B)
Vậy dt (MBC) = dt (NCB) mà tam giác MBC và tam giác NCB có chung đáy BC, nên chiều cao từ M bằng chiều cao từ N xuống đáy BC hay MN song song với BC. Do đó BMNC là hình thang.
Từ MB = 2/3 x AB, nên dt (MBN) = 2/3 x dt (ABN) (chung chiều cao từ N) hay dt (ABN) = 2/3 x dt (MBN).
Hơn nữa từ AC = 3 x AN, nên NC = 2 x AN, do đó dt (NBC) = 2 x dt (ABN) (chung chiều cao từ B) ; suy ra dt (NBC) = 3/2 x 2 x dt (MBN) = 3 x dt (MBN).
Mà tam giác NBC và tam giác MBN có chiều cao bằng nhau (cùng là chiều cao của hình thang BMNC). Vì vậy đáy BC = 3 x MN.
b) Gọi BN cắt CM tại O. Ta sẽ chứng tỏ AI cũng cắt BN tại O. Muốn vậy, nối AO kéo dài cắt BC tại K, ta sẽ chứng tỏ K là điểm chính giữa của BC (hay K trùng với I).
Theo phần a) ta đã có dt (NBC) = 2 x dt (ABN). Mà tam giác NBC và tam giác ABN có chung đáy BN, nên chiều cao từ C gấp 2 lần chiều cao từ A xuống đáy BN. Nhưng đó là chiều cao tương ứng của hai tam giác BCO và BAO có chung đáy BO, vì vậy dt (BCO) = 2 x dt (BAO)
Tương tự ta cũng có dt (BCO) = 2 x dt (CAO).
Do đó dt (BAO) = dt (CAO). Hai tam giác BAO và CAO có chung đáy AO, nên chiều cao từ B bằng chiều cao từ C xuống đáy AO. Đó cũng là chiều cao tương ứng của hai tam giác BOK và COK có chung đáy OK, vì vậy dt (BOK) = dt (COK). Mà hai tam giác BOK và tam giác COK lại chung chiều cao từ O, nên hai đáy BK = CK hay K là điểm chính giữa của cạnh BC. Vậy điểm K trùng với điểm I hay BN, CM, AI cùng cắt nhau tại điểm O.
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Trên AB lấy điểm M, trên AC lấy điểm N sao cho AM = AN; gọi I là giao điểm của NB và MC. Chứng minh: tam giác ANB = tam giác AMC Cho tam giác ABC cân tại A .Trên AB lấy điểm M, trên AC lấy điểm N sao cho AM=AN;gọi I là giao điểm của NB và MC
a) Chứng minh: tam giác ANB = tam giác AMC
b) Chứng minh: MN // BC
c) Gọi D là trung điểm của BC .Chứng minh:A ,I ,D thẳng hàng
cả hình nữa nha
Xem chi tiết
a,Xét tam giác ABN và tam giác ACM có :
AM=AN (gt)
Góc A chung
AB=AC(gt)
=> tam giác ABN = tam giác ACM (c-g-c)
b,theo câu a =>AMC^=ANB^(1)
Ta có : AM=AN =>tam giác AMN cân tại A => AMN^=ANM^(2)
Từ 1 và 2 =>MNI^=NMI^(3)
Vì B1^=C1^
B^=C^
=>B^-B1^=C-C1^
=>C2^=B2^(4)
Mặt khác : I1^=I2^(đối đỉnh) (5)
Từ 3 ; 4 và 5 => MNI^+NMI^+I1^=180*=I2^+B2^+C2^(tổng 3 góc của 1 tam giác )
=> MNI^+NMI^ / 2 = B2^+C2^ / 2
=> B2^=MNI^
Vì 2 góc này ở vị trí sole trong và bằng nhau
=> MN // BC
Đúng 2
Bình luận (0)












