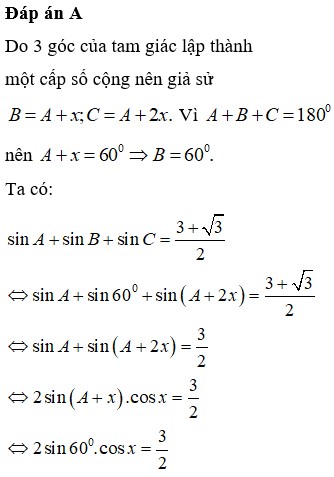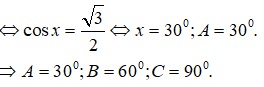cho tam giác abc có các góc B và C nhọn, AB=2AC. Tính tỉ số sin B : sin C

Những câu hỏi liên quan
a) Cho tam giác ABC có 3 góc nhọn. CMR: frac{a}{sin A}frac{b}{sin B}frac{c}{sin C}* Áp dụng : Cho Góc xOy 30 độ, A và B lần lượt là 2 điểm trên Ox và Oy sao cho AB1.Tính giá trị lớn nhất của độ dài OBb) Tam giác ABC có góc A nhọn. CMR: Scủa Tam giác ABCfrac{1}{2}b.c.sin A* Áp dụng: Cho tam giác ABC có góc A 40 độ, AB4 cm, AC7 cm. Tính S cua tam giác ABC.
Đọc tiếp
a) Cho tam giác ABC có 3 góc nhọn. CMR: \(\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\)
* Áp dụng : Cho Góc xOy =30 độ, A và B lần lượt là 2 điểm trên Ox và Oy sao cho AB=1.Tính giá trị lớn nhất của độ dài OB
b) Tam giác ABC có góc A nhọn. CMR: \(S\)của Tam giác ABC=\(\frac{1}{2}b.c.\sin A\)
* Áp dụng: Cho tam giác ABC có góc A = 40 độ, AB=4 cm, AC=7 cm. Tính S cua tam giác ABC.
Đã xảy ra lỗi rồi. Bạn thông cảm vì sai sót này.
Ta có:
Áp dụng hệ quả của bất đẳng thức Cauchy cho ba số không âm
trong đó với
, ta có:
Tương tự, ta có:
Cộng ba bất đẳng thức
và
, ta được:
Khi đó, ta chỉ cần chứng minh
Thật vậy, bất đẳng thức cần chứng minh được quy về dạng sau: (bất đẳng thức Cauchy cho ba số
)
Hay
Mà đã được chứng minh ở câu
nên
luôn đúng với mọi
Dấu xảy ra
Vậy,
Đúng 0
Bình luận (0)
Cho tam giác ABC có các góc B và C nhọn, AB=2AC. Tính tỉ số \(\sin\)B:\(\sin\)C
Kẻ đường cao AH, do B và C là các góc nhọn nên H nằm giữa B và C
Trong tam giác vuông ABH: \(sinB=\frac{AH}{AB}\)
Trong tam giác vuông ACH: \(sinC=\frac{AH}{AC}\)
\(\Rightarrow\frac{sinB}{sinC}=\frac{AH}{AB}.\frac{AC}{AH}=\frac{AC}{AB}=\frac{1}{2}\)
Đúng 0
Bình luận (0)
BÀI 1 :cho tam giác ABC vuông tại A có AB=4cm BC=6cm. tính tỉ số lượng giác của các góc B và C
BÀI 2 :đơn giản các biểu thức
a)\(A=\cos^2x+\cos^2x.\cot g^2x\)
b)\(sin^2x+\sin^2x.\tan^2x\)
c)\(\dfrac{2cos^2x-1}{\sin x+\cos x}\)
d)\(\dfrac{\cos x}{1+\sin x}+\tan x\)
Cho tam giác ABC biết ba góc tam giác lập thành cấp số cộng và
sin
A
+
sin
B
+
sin
C
3
+
3
2
.Tính các góc của tam giác A.
30
°
,
60
°
,
90
°
B.
20
°...
Đọc tiếp
Cho tam giác ABC biết ba góc tam giác lập thành cấp số cộng và sin A + sin B + sin C = 3 + 3 2 .Tính các góc của tam giác
A. 30 ° , 60 ° , 90 °
B. 20 ° , 60 ° , 100 °
C. 10 ° , 50 ° , 120 °
D. 40 ° , 60 ° , 80 °
Cho tam giác ABC vuông tại A có AB=c, BC=a, AC=b, đường cao AH. Lấy D nằm giữa A và C. Kẻ DE vuông góc với BC.
Chứng minh: \(\sin B=\frac{AB\cdot AD+EB\cdot ED}{BA\cdot BE+DA\cdot DE}\)
(Gợi ý cho những người không biết sin có thể làm luôn: Trong một tam giác vuông, sin góc nhọn bằng tỉ số cạnh đối chia cho cạnh huyền)
Bài 1 : cho tam giác ABC có góc A và B nhọn , các đg trung tuyến BM và CN vuông góc với nhau tại G . CMR :cotB+cotCgefrac{2}{3}Bài 2 Cho tam giác ABC có 3 góc nhọn có BCa,CAb,ABc. cmr a.a^2b^2+c^2-2bc.cosAb.sinfrac{A}{2}lefrac{a}{b+c}c.sinfrac{A}{2}.sinfrac{B}{2}.sinfrac{C}{2}lefrac{1}{8}
Đọc tiếp
Bài 1 : cho tam giác ABC có góc A và B nhọn , các đg trung tuyến BM và CN vuông góc với nhau tại G . CMR :\(cotB+cotC\ge\frac{2}{3}\)
Bài 2 Cho tam giác ABC có 3 góc nhọn có BC=a,CA=b,AB=c. cmr
a.\(a^2=b^2+c^2-2bc.cosA\)
b.\(sin\frac{A}{2}\le\frac{a}{b+c}\)
c.\(sin\frac{A}{2}.sin\frac{B}{2}.sin\frac{C}{2}\le\frac{1}{8}\)
Bài 1 : cho tam giác ABC có góc A và B nhọn , các đg trung tuyến BM và CN vuông góc vs nhau tại G . CMR :\(cotB+cotC\ge\frac{2}{3}\)
Bài 2 : Cho tam giác ABC có 3 góc nhọn có BC=a, CA=b, AB=c. CMR :
a.\(a^2=b^2+c^2-2bc.cosA\)
b.\(sin\frac{A}{2}\le\frac{a}{b+c}\)
c.\(sin\frac{A}{2}.sin\frac{B}{2}.sin\frac{C}{2}\le\frac{1}{8}\)
Từ A vẽ AD _|_ BC ,AG là trung tuyến cắt BC tại E\(\Rightarrow\)\(\hept{\begin{cases}AD\le AE\Rightarrow\frac{1}{AD}\ge\frac{1}{AE}\\1.2GE=BC\left(do\Delta BGCvuongcoElatrungdiem\right)\end{cases}}\)
cotB=\(\frac{BD}{AD}\)cotC=\(\frac{CD}{AD}\)\(\Rightarrow\)2.cotB + cotC=\(\frac{BC}{AD}\)
3.G là trực tâm nên 3GE=AE\(\Rightarrow\)\(\frac{1}{AD}\ge\frac{1}{3GE}\)
từ 1, 2 và 3 \(\Rightarrow\)cotB + cotC=\(\frac{BC}{AD}\ge\frac{2GE}{3GE}=\frac{2}{3}\)
Đúng 0
Bình luận (0)
\(\cot B+\cot C=\frac{BD}{AD}+\frac{CD}{AD}=\frac{BC}{AD}=\frac{BC}{3GH}\ge\frac{2GH}{3GH}=\frac{2}{3}\)
VỚI D LÀ CHÂN ĐƯỜNG CAO HẠ TỪ A XUÔNG BC , G LÀ TRỌNG TÂM , H LÀ CHÂN ĐƯỜNG CAO HẠ TỪ G XUỐNG BC
B2 THÌ GIẢI BÌNH THƯỜNG =='. ĐỌC THÊM NCPT 9 NHÉ
Đúng 0
Bình luận (0)
cho tam giác ABC thỏa mãn \(\sin^2A+\sin^2B=\sqrt{\sin C}\) và A, B là hai góc nhọn. chứng minh tam giác ABC vuông tại C
Cho tam giác vuông ABC có sin B = 0,5 , cạnh AB = 10cm.
a) Tính tỉ số lượng giác của góc C và độ dài cạnh AC.