
chứng minh đồng dạng giúp mik vs
GIẢI GIÚP MIK VS Ạ
cho tam giác abc nhọn (ab<ac) vẽ đường cao be và cf cắt nhau tại h.
a chứng minh tam giác abe đồng dạng với tam giác acf
b chứng minh he.hb=hf.hc
c. ah cắt bc tại d . Chứng minh: BH.BE+CH.CF=BC2
a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
góc BAE chung
=>ΔABE đồng dạng với ΔACF
b: Xét ΔHFB vuông tại F và ΔHEC vuông tại E có
góc FHB=góc EHC
=>ΔHFB đồng dạng với ΔHEC
=>HF/HE=HB/HC
=>HF*HC=HB*HE
Chứng minh: (n + 2)/13 và (n – 4)/13 không thể đồng thời là số nguyên.
Mn Giúp mik vs ;-;
Bài 4. (1,5 điểm)
Cho tam giác nhọn ABC
BD và CE là hai đường cao cắt nhau tại H.
a) Chứng minh rằng:
tam giác HED đồng dạng HBC
b) Chứng minh rằng:
tam giác ADE đồng dạng ABC
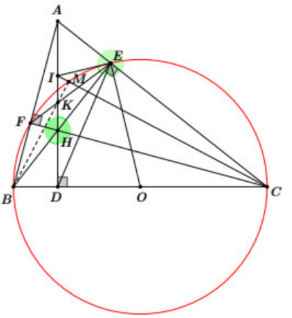
c) Gọi M là trung điểm của BC, qua H kẻ đường thẳng vuông góc với HM, cắt AB tại
I, cắt AC tại K. Chứng minh tam giác IMK là tam giác cân
giúp mik vs mn ơi


đây là đáp án bạn nhé

ảnh kia của mình nó bị thiếu nhé
Qua đỉnh A của hbh ABCD kẻ cát tuyến bất kì cắt BD và BC, DC tại E,F,G
a, chứng minh : tam giác DAE đồng dạng vs tam giác BFE
b, chứng minh : tam giác DGE đồng dạng vs tam giác BEA
c, chứng minh \(AE^2=EF.EG\)
c, chứng minh \(BF.BG\)không đổi
mn giúp e vs ạ
giúp mik vs câu 1 , cho tam giác ABC có AB bé hơn AC , các đường cao AE , BF cắt nhau tại H . gọi M là trung điểm của BC , qua H vẽ đường thẳng a vuông góc vs HM , a cắt AB và AC thứ tự ở I và K . CHỨNG MINH tam giác ABC đồng dạng vs tam giác EFC
Cho hình chữ nhật MNPQ. Gọi H là hình chiếu của M trên đường chéo NQ, K là trung điểm của HN
a) Chứng minh: Tg NMH đồng dạng với tg NQM
b) Chứng minh: PQ^2=NH.NQ
c) Gọi I là trung điểm của PQ. Tính góc MKI
giúp mik vs ạ ;-;
a: Xét ΔNMH vuông tại H và ΔNQM vuông tại M có
góc MNH chung
=>ΔNMH đồng dạng với ΔNQM
b: ΔNMH đồng dạng với ΔNQM
=>NH/NM=NM/NQ
=>NM^2=NH*NQ=PQ^2
c: Gọi A là trung điểm của HM
Xét ΔHMN có HK/HN=HA/HM=1/2
nên AK//MN và AK=1/2MN
=>AK//QI và AK=QI
=>AKIQ là hình bình hành
=>KA//QI
=>KA vuông góc MQ
Xét ΔMQK có
KA,MH là đường cao
KA cắt MH tại A
=>A là trực tâm
=>QA vuông góc MK
=>KI vuông góc KM
=>góc MKI=90 độ
giúp mik với ạ
Câu 15 (3,5 điểm ) Cho tam giác ABC vuông tại A, AB< AC, đường cao AH.
a) Chứng minh ABC đồng dạng với HAC.
b) Chứng minh HA = HB.HC c) Gọi M, N lần lượt là trung điểm của AB và BC. Chứng minh 4MN2 = HC. BC
d) Đường thẳng vuông góc với BC tại B cắt đường thắng MN tại O. Gọi I là giao điểm của AH vớiCO. Chứng minh I là trung điểm của AH.
chứng minh ADC đồng dạng vs BDH
Hoạc chứng minh IM.IC=2IE
Nêu hướng thôi cx đc
Xét tứ giác AEDB có: \(\widehat{AEB} = \widehat{ADB} = 90^o \)
⇒ Tứ giác AEDB nội tiếp (2 đỉnh E và D kề nhau cùng nhìn AB dưới 1 cặp góc bằng nhau)
⇒ \(\widehat{EAD} = \widehat{EBD} \) (cùng chắn \(\stackrel\frown{\text{ED}}\))
Xét ΔADC và ΔHDB có:
\(\widehat{ADC} = \widehat{HDB} = 90^o\)
\(\widehat{CAD} = \widehat{HBD} \) (cmt)
⇒ ΔADC ∼ ΔBDH (g-g)
Cho tam giác ABC nhọn 3 đường cao AH, BE, CD. Cắt nhau tại H. a) Tìm 12 cặp tam giác đồng dạng và chứng minh b) Chứng minh H là gđ của tam giác FED giúp mình vs ạ
a: Mình chỉ nêu ra thôi, chứng minh thì chắc chắn đều theo trường hợp g-g nha bạn
ΔADH đồng dạng vơi ΔAFB
ΔAEH đồng dạng với ΔAFC
ΔBFH đồg dạng với ΔBEC
ΔAFB đồng dạng vơi ΔBDC
ΔBEC đồng dạng với ΔAFC
ΔBAE đồng dạng với ΔCAD
ΔAHD đồng dạng với ΔCHF
ΔCHE đồng dạng với ΔBHD
ΔAHE đồng dạng vơi ΔBHF
ΔADE đồng dạng với ΔACB
ΔBDF đồng dạng với ΔBCA
ΔCFE đồng dạng với ΔCAB