|x| >3 khi nào
Những câu hỏi liên quan
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) \({x^2} - 2x - 3 > 0\) khi và chỉ khi \(x \in \left( { - \infty ; - 1} \right) \cup \left( {3; + \infty } \right)\)
b) \({x^2} - 2x - 3 < 0\) khi và chỉ khi \(x \in \left[ { - 1;3} \right]\)
Phương trình \({x^2} - 2x - 3 = 0\) có 2 nghiệm phân biệt \({x_1} = - 1,{x_2} = 3\)
Có \(a = 1 > 0\) nên
\(f\left( x \right) = {x^2} - 2x - 3 > 0\) khi và chỉ khi \(x \in \left( { - \infty ; - 1} \right) \cup \left( {3; + \infty } \right)\)
=> Phát biểu a) đúng.
\(f\left( x \right) = {x^2} - 2x - 3 < 0\) khi và chỉ khi \(x \in \left( { - 1;3} \right)\)
=> Phát biểu b) sai vì khi x=-1 hoặc x=3 thì \({x^2} - 2x - 3 = 0\) (không nhỏ hơn 0).
Đúng 0
Bình luận (0)
cho A=x2+\(\frac{4}{x^2+1}\)
Hỏi a,A>3 khi nào
b,A=3 khi nào
c,A<3 khi nào
\(A=x^2+\frac{4}{x^2+1}\)
\(=x^2+1+\frac{4}{x^2+1}-1\)
Áp dụng bất đẳng thức cauchy cho 2 số dương x^2 + 1 và 4 / x^2 + 1
\(x^2+1+\frac{4}{x^2+1}\ge2\sqrt{\left(x^2+1\right)\cdot\frac{4}{x^2+1}}\)
\(x^2+1+\frac{4}{x^2+1}\ge4\)
\(x^2+1+\frac{4}{x^2+1}-1\ge3\)
\(A\ge3\)
Dấu = xảy ra khi và chỉ khi
\(x^2+1=\frac{4}{x^2+1}\)
\(\left(x^2+1\right)^2=4\)
\(\orbr{\begin{cases}x^2+1=2\\x^2+1=-2\end{cases}}\)
\(\orbr{\begin{cases}x^2=1\\x^2=-3\left(sai\right)\end{cases}}\)
\(\orbr{\begin{cases}x=1\\x=-1\end{cases}}\)
Vậy A > 3 khi x khác 1 và - 1
A = 3 khi x = 1 hay x = - 1
A < 3 vô nghiệm
Cho hàm số
f
(
x
)
x
2
-
5
k
h
i
x
≥
3
...
Đọc tiếp
Cho hàm số f ( x ) = x 2 - 5 k h i x ≥ 3 ( 1 ) x 2 - 5 x + 2 k h i x < 3 ( 2 )
Trong biểu thức (2) ở trên, cần thay số 5 bằng số nào để hàm số f(x) có giới hạn khi x → 3?
A. 19.
B. 1.
C. -1.
D. Không có số nào thỏa mãn.
Chọn C.
Hàm số đã cho các định trên R \ {2}.
Ta có 
Đặt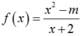 
khi x < 3 (m là tham số, m > 0).
Ta có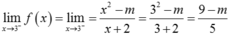 
.
Để hàm số f(x) có giới hạn khi x → 3 thì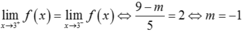 
.
Đúng 0
Bình luận (0)
Cho hàm số f(x)
3
-
x
2
2
k
h
i
x
1...
Đọc tiếp
Cho hàm số f(x)= 3 - x 2 2 k h i x < 1 1 x k h i x ≥ 1 . Khẳng định nào dứoi đây là sai
A. Hàm số f(x) liên tục tại x= 1
B. Hàm số f(x) có đạo hàm tại x= 1
C. Hàm số f(x) liên tục và có đạo hàm tại x= 1
D. Hàm số f(x) không có đạo hàm tại x= 1
Cho hàm số
f
x
x
+
x
+
2
x
+
1
,
k...
Đọc tiếp
Cho hàm số f x = x + x + 2 x + 1 , k h i x > - 1 2 x + 3 , k h i x ≤ - 1 . Khẳng định nào sau đây đúng nhất:
A. Hàm số liên tục tại x= -1.
B. Hàm số liên tục tại mọi điểm.
C. Hàm số gián đoạn tại x= -1.
D. Tất cả đều sai.
Ta có : f − 1 = 1 và lim x → − 1 − f x = lim x → − 1 − ( 2 x + 3 ) = 2. ( − 1 ) + 3 = 1
lim x → − 1 + f x = lim x → − 1 + x + x + 2 x + 1 = lim x → − 1 + x 2 − x − 2 x + 1 x − x + 2 = lim x → − 1 + x − 2 x − x + 2 = 3 2
Suy ra : lim x → − 1 + f x ≠ lim x → − 1 − f x
Vậy hàm số gián đoạn tại x= -1.
Chọn đáp án C
Đúng 0
Bình luận (0)
Cho hàm số
f
(
x
)
x
+
x
+
2
x
+
1
...
Đọc tiếp
Cho hàm số f ( x ) = x + x + 2 x + 1 K h i x > - 1 2 x + 3 k h i x ≤ - 1 . Khẳng định nào sau đây đúng nhất.
A. Hàm số liên tục tại tại tại x0 = -1
B. Hàm số liên tục tại mọi điểm
C. Hàm số không liên tục tại tại x0 = -1.
D. Tất cả đều sai
Chọn C.
Ta có: f(-1) = 1 và 
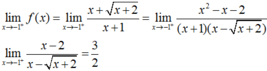
Suy ra 
Vậy hàm số không liên tục tại x0 = -1.
Đúng 0
Bình luận (0)
Cho hàm số
f
x
3
−
4
−
x
4
k
h
i
x...
Đọc tiếp
Cho hàm số f x = 3 − 4 − x 4 k h i x ≠ 0 1 4 k h i x = 0 . Khi đó f '(0) là kết quả nào sau đây?
A. 1 4
B. 1 16
C. 1 32
D. Không tồn tại
Đáp án B
lim x → x 0 f x − f x 0 x − x 0 = lim x → 0 3 − 4 − x 4 − 1 4 x − 0 = lim x → 0 2 − 4 − x 4 x = lim x → 0 1 4 2 + 4 − x = 1 16
Đúng 0
Bình luận (0)
Cho hàm số
f
x
3
-
4
-
x
4
k
h
i
x...
Đọc tiếp
Cho hàm số f x = 3 - 4 - x 4 k h i x ≠ 0 1 4 k h i x = 0 Khi đó f'(0) là kết quả nào sau đây?
A. 1 4
B. 1 16
C. 1 32
D. Không tồn tại
Cho hàm số
f
(
x
)
x
2
-
x
-
2
x
-
2...
Đọc tiếp
Cho hàm số f ( x ) = x 2 - x - 2 x - 2 + 2 x k h i x > 2 x 2 - x + 3 k h i x ≤ 2 Khẳng định nào sau đây đúng nhất
A. Hàm số liên tục tại x = 2
B. Hàm số liên tục tại mọi điẻm
C. Hàm số không liên tục tại x = 2
D. Tất cả đều sai
Chọn C.
Ta có:
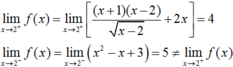
Hàm số không liên tục tại x = 2.
Đúng 0
Bình luận (0)