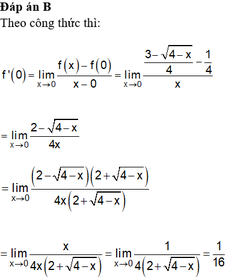Các câu hỏi tương tự
Cho hàm số
f
x
3
−
4
−
x
4
k
h
i
x...
Đọc tiếp
Cho hàm số f x = 3 − 4 − x 4 k h i x ≠ 0 1 4 k h i x = 0 . Khi đó f '(0) là kết quả nào sau đây?
A. 1 4
B. 1 16
C. 1 32
D. Không tồn tại
Cho hàm số
f
x
3
−
4
−
x
4
khi
x
≠
0...
Đọc tiếp
Cho hàm số f x = 3 − 4 − x 4 khi x ≠ 0 1 4 khi x = 0 . Khi đó f'(0) là kết quả nào sau đây?
A. 1 16
B. Không tồn tại
C. 0
D. 1 4
Cho hàm số yf(x) có bảng xét dấu của đạo hàm như sau.x -∞ -2 -1 2 4 +∞f’(x) + 0 - 0 + 0 - 0 + Hàm số y -2f(x)+2019 nghịch biến trên khoảng nào trong các khoảng dưới đây? A. (-4 ;2) B. (-1 ;2) C. (-2 ;-1) D. (2 ;4)
Đọc tiếp
Cho hàm số y=f(x) có bảng xét dấu của đạo hàm như sau.
x -∞ -2 -1 2 4 +∞
f’(x) + 0 - 0 + 0 - 0 +
Hàm số y =-2f(x)+2019 nghịch biến trên khoảng nào trong các khoảng dưới đây?
A. (-4 ;2)
B. (-1 ;2)
C. (-2 ;-1)
D. (2 ;4)
Cho hàm số yf(x) có đạo hàm
f
(
x
)
x
2
(
x
-
1
)
(
x
-
4
)
g
(
x
)
, trong đó
g
(
x
)
0
,
∀
x
. Hàm số
y
f
(
x
2...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = x 2 ( x - 1 ) ( x - 4 ) g ( x ) , trong đó g ( x ) > 0 , ∀ x . Hàm số y = f ( x 2 ) đồng biến trên khoảng nào dưới đây?
A. ( - ∞ ; - 2 ) .
B. (-1;1).
C. (-2;-1).
D. (1;2).
Cho hàm số f (x) có đồ thị của hàm số f(x) như hình vẽ bên.Biết f(-1)f(4)0. Hàm số
y
(
f
(
x
)
)
2
nghịch biến trên khoảng nào dưới đây ? A. (-1;0). B. (1;4). C.
(
-
∞
;
1
)
. D.
(
4
;
+
∞
)
.
Đọc tiếp
Cho hàm số f (x) có đồ thị của hàm số f'(x) như hình vẽ bên.
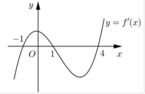
Biết f(-1)=f(4)=0. Hàm số y = ( f ( x ) ) 2 nghịch biến trên khoảng nào dưới đây ?
A. (-1;0).
B. (1;4).
C. ( - ∞ ; 1 ) .
D. ( 4 ; + ∞ ) .
Cho hàm số
f
x
x
. Để tính f (0), bạn Thảo Huyền đã trình bày lời giải trên bảng theo các bước sauBước 1:
f
x
x
x
x
0
0...
Đọc tiếp
Cho hàm số f x = x . Để tính f '(0), bạn Thảo Huyền đã trình bày lời giải trên bảng theo các bước sau
Bước 1: f x = x = x x > 0 0 x = 0 - x x < 0
Bước 2:
f ' 0 + = lim x → 0 + f x - f 0 x - 0 = lim x → 0 + x - 0 x - 0 = 1
Bước 3:
f ' 0 - = lim x → 0 - f x - f 0 x - 0 = lim x → 0 - x - 0 x - 0 = 1
Bước 4: f ' 0 + = f ' 0 - = 1
Vậy f ' (0) = 1
Sau khi quan sát trên bảng, bạn Duy Lĩnh đã phát hiện ra rằng trong lời giải của bạn Thảo Huyền có một bước bị sai sót. Vậy sai sót đó từ bước nào?
A. Bước 1
B.Bước 2
C. Bước 3
D. Bước 4
Cho hàm số
y
f
(
x
)
a
x
3
+
b
x
2
+
c
x
+
d
(a;b;c;d
∈
R, a
≠...
Đọc tiếp
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d (a;b;c;d ∈ R, a ≠ 0) có đồ thị (C). Biết rằng đồ thị (C) đi qua gốc tọa độ và có đồ thị hàm số y = f’(x) cho bởi hình vẽ sau đây.

Tính giá trị H = f(4) – f(2)
A. H = 51
B. H = 54
C. H = 58
D. H = 64
Cho hàm số f(x) xác định trên R{0;2}thỏa mãn
f
x
2
x
2
-
2
x
;
f
-
1
+
f
3
2
và f(1) 0.Tính f(-2) + f(3/2) +f(4), được kết quả: A. 1 + ln3 B. 2 + ln3 C. 2 – ln3 D. 1 – ln3
Đọc tiếp
Cho hàm số f(x) xác định trên R\{0;2}thỏa mãn f ' x = 2 x 2 - 2 x ; f - 1 + f 3 = 2 và f(1) = 0.Tính f(-2) + f(3/2) +f(4), được kết quả:
A. 1 + ln3
B. 2 + ln3
C. 2 – ln3
D. 1 – ln3
Cho biết yf(x) là hàm số liên tục và xác định trên R|{1;3} và thỏa mãn đồng thời các điều kiện:
f
(
x
)
1
(
x
-
1
)
(
x
-
3
)
;
f
(
0
)
2
f
(
2
)...
Đọc tiếp
Cho biết y=f(x) là hàm số liên tục và xác định trên R|{1;3} và thỏa mãn đồng thời các điều kiện: f ' ( x ) = 1 ( x - 1 ) ( x - 3 ) ; f ( 0 ) = 2 f ( 2 ) = 4 f ( 4 ) = 4 Khi đó giá trị của biểu thức: f ( - 1 ) + f 3 2 + f 9 2 nằm trong khoảng?
A . 5 - 1 2 ln 7 18
B . 7 - 1 2 ln 7 18
C . 2 + 1 2 ln 7 18
D . 3 + 1 2 ln 7 18