Các câu hỏi tương tự
Tìm họ nguyên hàm của hàm số lượng giác sau :
\(f\left(x\right)=\int\frac{4\sin x+3\cos x}{\sin x+2\cos x}dx\)
Biết
F
(
x
)
(
a
x
2
+
b
x
+
c
)
e
-
x
là một nguyên hàm của hàm số
f
(
x
)
(
2
x
2
-
5
x
+
2
)
e
-...
Đọc tiếp
Biết F ( x ) = ( a x 2 + b x + c ) e - x là một nguyên hàm của hàm số f ( x ) = ( 2 x 2 - 5 x + 2 ) e - x trên R. Giá trị của biểu thức f(F(0)) bằng
A. 9e
B. 3e
C. 20 e 2
D. - 1 e
Xác định giá trị a, b, c để hàm số
F
(
x
)
(
a
x
2
+
b
x
+
c
)
e
-
x
là một nguyên hàm của
f
(
x
)
(
x
2
-
3
x
+
2
)
e...
Đọc tiếp
Xác định giá trị a, b, c để hàm số F ( x ) = ( a x 2 + b x + c ) e - x là một nguyên hàm của f ( x ) = ( x 2 - 3 x + 2 ) e - x
A. a = -1; b = 1; c = -1
B. a = -1; b = -5; c = -7
C. a = 1; b = -3; c = 2
D. a = 1; b = -1; c = 1
Cho hai hàm số F(x)
(
x
2
+
a
x
+
b
)
e
-
x
v
à
f
(
x
)
(
-
x
2
+
3
x
+
6
)
e
-
x
. Tìm a và b đ...
Đọc tiếp
Cho hai hàm số F(x)= ( x 2 + a x + b ) e - x v à f ( x ) = ( - x 2 + 3 x + 6 ) e - x . Tìm a và b để F(x) là một nguyên hàm của hàm số f(x)
A. a=1;b= -7
B. a= -1;b= -7
C. a= -1;b=7
D. a=1;b=7
Cho hàm số
f
(
x
)
a
x
4
+
b
x
3
+
c
x
3
+
d
x
+
e
(
a
≠
0
)
. Biết rằng hàm số f(x) có đạo hàm là f’(x) và hàm số yf’(x) có đồ thị như hình vẽ dưới. Khi đó mệnh đề nào sau đây sai? A. Hàm số f(x) nghịch biến trên khoảng (-1;1...
Đọc tiếp
Cho hàm số f ( x ) = a x 4 + b x 3 + c x 3 + d x + e ( a ≠ 0 ) . Biết rằng hàm số f(x) có đạo hàm là f’(x) và hàm số y=f’(x) có đồ thị như hình vẽ dưới. Khi đó mệnh đề nào sau đây sai?
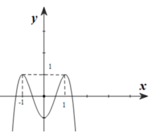
A. Hàm số f(x) nghịch biến trên khoảng (-1;1)
B. Hàm số f(x) đồng biến trên khoảng (0;+∞)
C. Hàm số f(x) đồng biến trên khoảng (-2;1)
D. Hàm số f(x) nghịch biến trên khoảng (-∞;-2)
Một nguyên hàm F(x) của hàm số
f
(
x
)
e
-
x
+
e
x
2
thỏa mãn F(0) 1 là
Đọc tiếp
Một nguyên hàm F(x) của hàm số f ( x ) = e - x + e x 2 thỏa mãn F(0) = 1 là
![]()
![]()
![]()
![]()
Cho các mệnh đề sau đây:(1) Hàm số
f
(
x
)
log
2
2
x
-
log
2
x
4
+
4
có tập xác định
D
[
0
;
+
∞
)
(2) Hàm số
y
log
a
x
có tiệm cận ngang(3) Hàm số
y
log
a
x
;
...
Đọc tiếp
Cho các mệnh đề sau đây:
(1) Hàm số f ( x ) = log 2 2 x - log 2 x 4 + 4 có tập xác định D = [ 0 ; + ∞ )
(2) Hàm số y = log a x có tiệm cận ngang
(3) Hàm số y = log a x ; 0 < a < 1 và Hàm số y = log a x , a > 1 đều đơn điệu trên tập xác định của nó
(4) Bất phương trình: log 1 2 5 - 2 x 2 - 1 ≤ 0 có 1 nghiệm nguyên thỏa mãn.
(5) Đạo hàm của hàm số y = ln 1 - cos x là sin x 1 - cos x 2
Hỏi có bao nhiêu mệnh đề đúng:
A. 0
B. 2
C. 3
D.1
Cho hàm số f(x) là một nguyên hàm của hàm số y
e
x
x
≥
1
e
-
x
...
Đọc tiếp
Cho hàm số f(x) là một nguyên hàm của hàm số y = e x x ≥ 1 e - x x ≤ 1 với f(1)=e. Giá trị biểu thức f(-ln3)+f(-ln2)+f(ln2)+f(ln3) bằng
A. 2 e + 1 e
B. 3 e + 1 e - 10 3
C. 3 e + 1 e - 5 2
D. 3 e + 1 e + 21 2
Tìm nguyên hàm F(x) của hàm số
f
(
x
)
3
x
2
−
e
−
x
thỏa mãn
F
(
0
)
3
. A.
F
(
x
)
x
3
−
e
−
x
−
3...
Đọc tiếp
Tìm nguyên hàm F(x) của hàm số f ( x ) = 3 x 2 − e − x thỏa mãn F ( 0 ) = 3 .
A. F ( x ) = x 3 − e − x − 3
B. F ( x ) = x 3 + e − x + 2
C. F ( x ) = x 3 − e − x + 3
D. F ( x ) = x 3 + e − x − 2