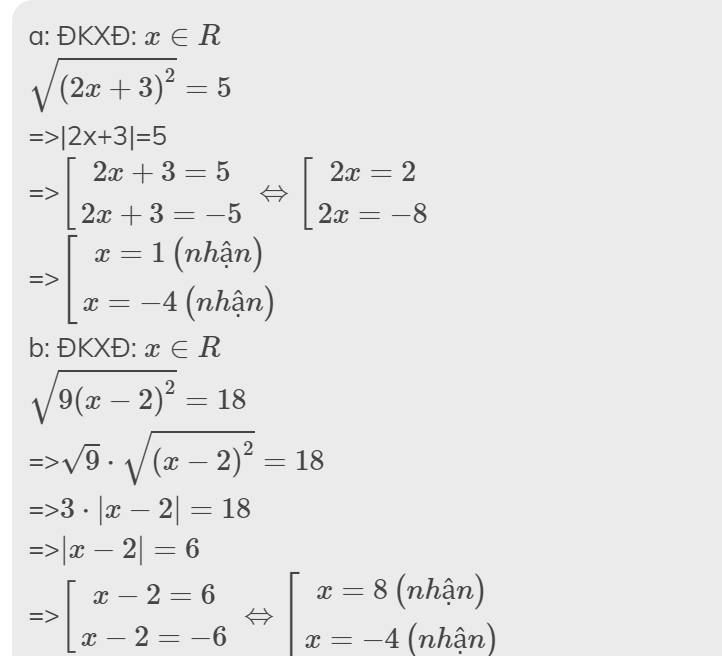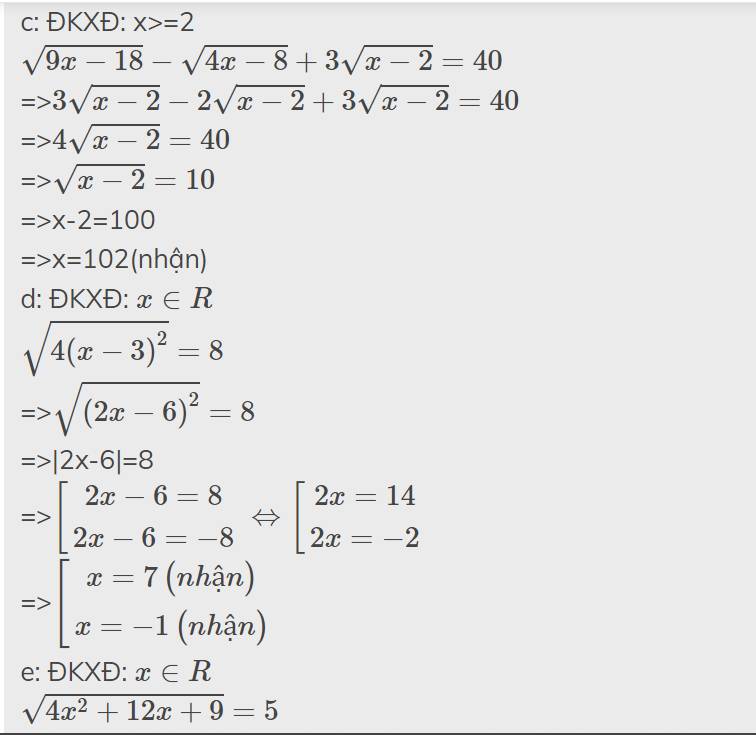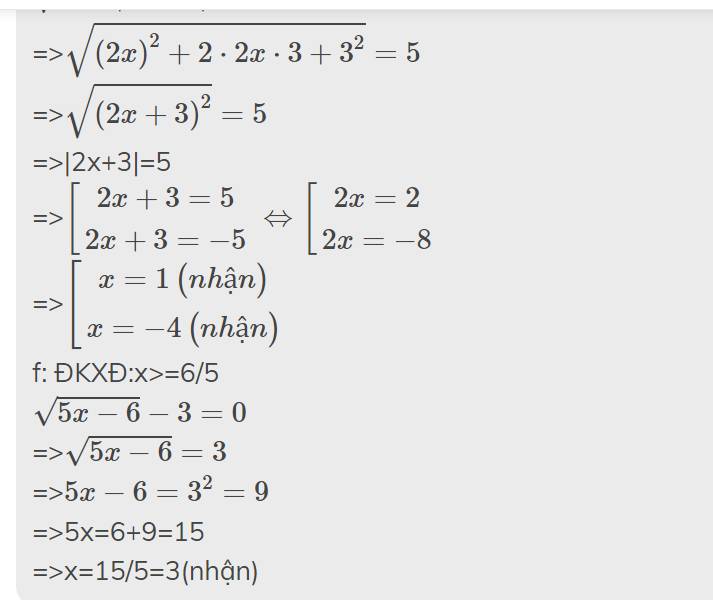Giải phương trình: \(\left(x-2\right).\left(5x^2+10x-34\right)=18\sqrt{5x-1}.\sqrt[3]{x-1}-27x\)
Những câu hỏi liên quan
27 tháng 11 2021 lúc 15:51
Giải phương trình:
a) \(5x^2-10x=4\left(x-1\right)\sqrt{x^2-2x+2}\)
b) \(\sqrt{2x^2+22x+29}-x-2=2\sqrt{2x+3}\)
c) \(x^3-7x^2+9x+12=\left(x-3\right)\left(x-2+5\sqrt{x-3}\right)\left(\sqrt{x-3}-1\right)\)
Giải phương trình:
a) \(\left(\sqrt{x^2+x+1}+\sqrt{4x^2+x+1}\right)\left(\sqrt{5x^2+1}-\sqrt{2x^2+1}\right)=3x^2\)
b) \(\sqrt{8x+1}+\sqrt{46-10x}=-x^3+5x^2+4x+1\)
Giải hệ phương trình sau
\(\left\{{}\begin{matrix}\sqrt{x+1}+\sqrt{4-2y}+\sqrt{5+2y-\left(x-1\right)^2}\\5x^4+\left(x-y\right)^2=\left(10x^3+y\right)y\end{matrix}\right.\)
giải phương trình :
a, \(\left(\sqrt{5x-1}+\sqrt{x-1}\right)\left(3x-1-\sqrt{5x^2-6x+1}\right)=4x\)
b, \(2\left(\sqrt{x}-\sqrt{x-1}\right)\left(1+\sqrt{x^2-1}\right)=x\sqrt{x}\)
giải phương trình :
a, \(\left(\sqrt{5x-1}+\sqrt{x-1}\right)\left(3x-1-\sqrt{5x^2}-6x+1\right)=4x\)
b, \(2\left(\sqrt{x}-\sqrt{x-1}\right)\left(1+\sqrt{x^2-1}\right)=x\sqrt{x}\)
13 tháng 3 2020 lúc 21:50
Giải hệ phương trình sau:
\(\hept{\begin{cases}\sqrt{x+1}+\sqrt{4-2y}+\sqrt{5+2y-\left(x-1\right)^2}=5\\5x^4+\left(x-y\right)^2=\left(10x^3+y\right)y\end{cases}}\)
Phương trình thứ hai tương đương: \(5x^4-10x^3y+x^2-2xy=0\Leftrightarrow5x^3\left(x-2y\right)+x\left(x-2y\right)=0\Leftrightarrow x\left(x-2y\right)\left(5x^2+1\right)=0\)
Vì \(5x^2+1>0\)nên \(x\left(x-2y\right)=0\Leftrightarrow\orbr{\begin{cases}x=0\\x=2y\end{cases}}\)
Đến đây bạn tự giải tiếp
Giải Phương Trình
\(\sqrt{\left(2x+3\right)^2}=5\)
\(\sqrt{9\left(x-2\right)^2}=18\)
\(\sqrt{9x-18}-\sqrt{4x-8}+3\sqrt{x-2}=40\)
\(\sqrt{4.\left(x-3\right)^2}=8\)
\(\sqrt{5x-6}-3=0\)
6 tháng 11 2021 lúc 21:47
Giải phương trình sau : \(x^2-x-18+\left(2x+9\right)\sqrt{x+3}-2\sqrt{5x-1}=0\)
Giải phương trình: \(2\left(5x-3\right)\sqrt{x+1}+5\left(x+1\right)\sqrt{3-x}=3\left(5x+1\right)\)
\(Đk:-1\le x\le3\)
Đặt: \(\hept{\begin{cases}u=\sqrt{x+1}\\v=\sqrt{3-x}\end{cases}}\) Ta suy ra:
\(u^2=x+1\)
\(3u^2-2v^2=5x-3\)
\(4u^2-v^2=5x+1\)
\(u^2+v^2=4\)
Pt đã cho trở thành:
\(2\left(3u^2-2v^2\right)+5uv^2=3\left(4u^2-v^2\right)\Leftrightarrow6u^2\left(2-u\right)=v^2\left(u+3\right)\)
Thay \(v^2=4-u\) ta thu được pt:
\(2\left(3u^2-2v^2\right)+5uv^2=3\left(4u^2-v^2\right)\)
\(\Leftrightarrow6u^2\left(2-u\right)=\left(4-u^2\right)\left(u+3\right)\Leftrightarrow\orbr{\begin{cases}u=2\\u=\frac{5+\sqrt{145}}{10}\end{cases}}\)
Từ đó tìm đc các nghiệm của pt là: \(\orbr{\begin{cases}x=3\\x=\frac{7+\sqrt{145}}{10}\end{cases}}\)
Sai r bn ơi
Sao thay vào lại đc 5uv^2 vậy ạ phải là 5u^2v chứ