Cho hình chóp S.ABCD đáy là hình vuông, SA vuông góc với (ABCD) a) CMR : BC vuông góc với (SAB); CD vuông góc với (SAD) b) CMR : BD vuông góc với (SAC) c) Kẻ AE vuông góc với SB. CMR : SB vuông góc với (ADE)

Những câu hỏi liên quan
Cho hình chóp S.ABCD , đáy ABCD là hình thang vuông tại A và D . SA vuông góc với (ABCD ) , AD=DC=AB/2=a , SA=a căn 3. Gọi I là trung điểm AB. CMR a. CI vuông góc (SAB ) , DI vuông góc (SAC) b. Các mặt bên hình chóp là những tam giác vuông
Cho chóp S.ABCD đáy là hình chữ nhật. SA vuông góc đáy, SA=a√5;AD=2AB=4a.
a, Chứng minh BC vuông góc với mp (SAB).
b, Tính (SB;(ABCD).
(SC;(ABCD).
(SD;ABCD).
a: BC vuông góc AB; BC vuông góc SA
=>BC vuông góc (SAB)
b: (BS;(BACD))=(BS;BA)=góc SBA
tan SBA=SA/AB=căn 5/2
=>góc SBA=48 độ
(SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=1
=>góc SCA=45 độ
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD với ABCD là hình vuông cạnh a ,SA vuông góc với đáy, SA=a. Tính góc giữa 2 mp (SAB) và (SCD)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, S A = a 2 . Tính góc giữa SC và mp (SAB).
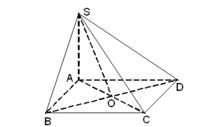
● BC ⊥ (SAB) ⇒ 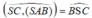
● ΔSAB vuông tại A 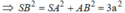
● ΔSBC vuông tại B 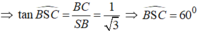
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a có cạnh SA=a căn 2 và SA vuông góc với mặt phẳng với (ABCD).Tính a) Góc giữa đường thẳng BC và mặt phẳng (SAB) b)Góc giữa đường thẳng DC và mặt phẳng (SAB)
cho hình chóp S.ABCD có đáy là hình vuông SA vuông góc (ABCD). gọi M là hình chiếu vuông góc của A lên cạnh SB cmr: a, CB vuông góc (SAB) b, AM vuông góc (SBC)
a: CB vuông góc SA
CB vuông góc AB
=>CB vuông góc (SAB)
b: CB vuông góc (SAB)
=>CB vuông góc AM
mà AM vuông góc SB
nên AM vuông góc (SBC)
Đúng 1
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, cạnh SA vuông góc với đáy và mặt phẳng (SAB) tạo với đáy một góc 60 ° . Tính thể tích khối chóp S.ABCD.
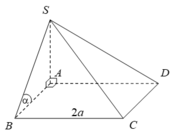
Ta có: SA ⊥ (ABCD) SA ⊥ AB
Mặt phẳng (SAB) tạo với đáy một góc 60° nên
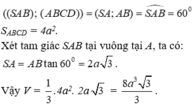
Đúng 0
Bình luận (0)
Câu4: cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh. Cạnh bên SB vuông góc với đáy.
a/ chứng minh BC vuông (SAB)
b/ chứng minh BC vuông SA
\(\left\{{}\begin{matrix}SB\perp\left(ABCD\right)\Rightarrow SB\perp BC\\BC\perp AB\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\left\{{}\begin{matrix}BC\perp\left(SAB\right)\\SA\in\left(SAB\right)\end{matrix}\right.\) \(\Rightarrow BC\perp SA\)
Đúng 0
Bình luận (0)
cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với đáy SA=a căn 3 a)cm SAC vuông góc với SBD b)gọi AH là đg cao của tam giác SAB . cmr AK vuông góc với (SBC) c) tính góc giữa đg thẳng SC và mặt đáy ABC d) tính khoảng cách từ a đến mp (SCD)
a: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
b: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
=>BC vuông góc AK
mà AK vuông góc SB
nên AK vuông góc (SBC)
Đúng 0
Bình luận (0)













