Cho tam giác ABC có
AB=4,AC=6,BC=8
Lấy D thuộc BC sao cho
DB = 2, Tính độ dài đoạn
AD
Những câu hỏi liên quan
cho tam giác abc có
ab=5cm
ac=6cm
góc c =30. tính độ dài bc
kẻ đường cao AH ( H ϵ BC)
trong tam giác vuông AHC:
\(\sin C\) = \(\dfrac{AH}{AC}\) ⇒ AH = AC.\(\sin C\) = 6\(\sin\left(30\right)\) = 3 cm
HC = \(\sqrt{AC^2-AH^2}\) = \(\sqrt{6^2-3^2}\) = 3\(\sqrt{3}\) cm
Trong tam giác vuông BHC:
BH = \(\sqrt{AB^2-AH^2}\) = \(\sqrt{5^2-3^2}\) = 4 cm
BC = HC + BH = 4 + 3\(\sqrt{3}\)
Đúng 1
Bình luận (1)
Tam giác ABC có AB = 4; BC = 6 và A C = 2 7 . Điểm M thuộc đoạn BC sao cho MC = 2MB. Tính độ dài cạnh AM.
A. 4
B. 3
C. 2 3
D.Đáp án khác
Chọn C.
Theo định lí hàm cosin, ta có : 
Do MC = 2MB nên BM = 1/3.BC = 2.
Theo định lí hàm cosin, ta có: AM2 = AB2 + BM2 - 2AB.BM.cos B = 42 + 22 -2.4.2.1/2 = 12
Do đó: 
.
Đúng 0
Bình luận (0)
Cho tam giác ABC có
AB=8,AC=6,BC=10. Đường tròn tâm I nội tiếp tam giác ABC. Tính AI?
Ta có : \(BC^2=AB^2+AC^2\Leftrightarrow100=64+36\)(luôn đúng)
vậy tam giác ABC vuông tại A
tâm đường tròn nội tiếp tam giác ABC vuông tại A là trung điểm cạnh huyền
hay AI = IB = IC = BC/2 = 5
Đúng 4
Bình luận (1)
cho tam giác ABC cóAB=6 cm,BC=8cm,^B=2^C. TÍNH AC
tam giác ABC có AB=4,BC=6,AC=\(2\sqrt{7}\).Điểm M thuộc đoạn BC sao cho MC=2MB.Tính độ dài cạnh AM
Cho tam giác ABC có:AB=9cm,AC=12cm.Lấy D thuộc AB, E thuộc AC sao cho AD=3cm;AE=4cm a,CM:tam giác ABC đồng dạng với tam giác ADE b,DE//BC c,Cho BE là phân giác của góc ABC.Tính BC d,Tính độ dài DE (Vẽ hình ạ)
a: Xét ΔABC và ΔADE có
AB/AD=AC/AE
góc A chung
=>ΔABC đồng dạng với ΔADE
b: ΔBAC đồng dạng với ΔDAE
=>góc ABC=góc ADE
=>BC//DE
c: AE+EC=AC
=>EC=8cm
BE là phân giác góc ABC
=>AB/AE=BC/CE
=>BC/8=9/4
=>BC=18cm
d: DE//BC
=>DE/BC=AE/AC=1/3
=>DE/18=1/3
=>DE=6cm
Đúng 0
Bình luận (0)
cho tam giác ABC có AB= 6cm, AC= 5cm, BC=9cm. Điểm D thuộc cạnh BC sao cho BD= 4cm. Tính độ dài AD
Xét ΔBDA và ΔBAC có
\(\dfrac{BD}{BA}=\dfrac{BA}{BC}\)
\(\widehat{B}\) chung
Do đó: ΔBDA~ΔBAC
=>\(\dfrac{AD}{AC}=\dfrac{BD}{BA}\)
=>\(\dfrac{AD}{5}=\dfrac{4}{6}=\dfrac{2}{3}\)
=>\(AD=5\cdot\dfrac{2}{3}=\dfrac{10}{3}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = 12cm, AC = 18cm, BC = 27cm. Điểm D thuộc cạnh BC sao cho CD = 12cm. Tính độ dài AD.
A. 12cm
B. 6cm
C. 10cm
D. 8cm
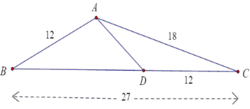
Ta có
A C D C = 18 12 = 3 2 , C B C A = 27 18 = 3 2 ⇒ C A C D = C B C A
Xét ΔACB và ΔDCA có góc C chung và C A C D = C B C A (cmt)
Nên ΔACB ~ ΔDCA (c.g.c)
⇒ A C D C = A B D A ⇔ 3 2 = 12 D A ⇒ D A = 2.12 3 = 8 c m
Đáp án: D
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A (AB<AC),đường cao AH (H thuộc BC).
a) Chứng minh: tam giác HBA đồng dạng tam giác ABC
b) Chứng minh: AB2=BC.HB
c) gọi BD là phân giác của ABC (D thuộc BC) sao cho AD= 3cm Dc= 5 cm. TÍnh độ dài các đoạn thẳng AB, BC
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: ΔHBA đồng dạng với ΔABC
=>BH/BA=BA/BC
=>BA^2=BH*BC
Đúng 0
Bình luận (0)