\(2A=2+2^2+2^3+2^4+2^5+...+2^{2022}\)

\(A=2A-A=2^{2022}-1\)

bạn ơi câu này thêm 2^5 vào à

    1. Phương pháp 1: ( Hình 1)

        Nếu  thì ba điểm A; B; C thẳng hàng.

    2. Phương pháp 2: ( Hình 2)

        Nếu AB // a và AC // a thì ba điểm A; B; C thẳng hàng.

       (Cơ sở của phương pháp này là: tiên đề Ơ – Clit- tiết 8- hình 7)

    3. Phương pháp 3: ( Hình 3)

        Nếu AB  a ; AC  A thì ba điểm A; B; C thẳng hàng.

        ( Cơ sở của phương pháp này là: Có một và chỉ một đường thẳng

        a^’ đi qua điểm O và vuông góc với đường thẳng a cho trước

        - tiết 3 hình học 7)

        Hoặc A; B; C cùng thuộc một đường trung trực của một

        đoạn thẳng .(tiết 3- hình 7)

    4. Phương pháp 4: ( Hình 4)

        Nếu tia OA và tia OB là hai tia phân giác của góc xOy

        thì ba điểm O; A; B thẳng hàng.

        Cơ sở của phương pháp này là:                                                        

        Mỗi góc có một và chỉ một tia phân giác .

     * Hoặc : Hai tia OA và OB cùng nằm trên nửa mặt phẳng bờ chứa tia Ox ,

                   thì ba điểm O, A, B thẳng hàng.

    5. Nếu K là trung điểm BD, K^’ là giao điểm của BD và AC. Nếu K^’

       Là trung điểm BD  thì K^’  K thì A, K, C thẳng hàng.

      (Cơ sở của phương pháp này là: Mỗi đoạn thẳng chỉ có một trung điểm)

C. Các ví dụ minh họa cho tùng phương pháp:

                                                                Phương pháp 1

    Ví dụ 1. Cho tam giác ABC vuông ở A, M là trung điểm AC. Kẻ tia Cx vuông góc CA

                     (tia Cx và điểm B ở hai nửa mặt phẳng đối nhau bờ AC). Trên tia Cx lấy điểm

                     D sao cho CD = AB.

                     Chứng minh ba điểm B, M, D thẳng hàng.

     Gợi ý: Muốn B, M, D thẳng hàng cần chứng minh

               Do nên cần chứng minh

BÀI GIẢI:

               AMB và CMD có:                                                       

                   AB = DC (gt).

                    MA = MC (M là trung điểm AC)                                              

               Do đó: AMB = CMD (c.g.c). Suy ra:

               Mà   (kề bù) nên .

               Vậy ba điểm B; M; D thẳng hàng.

    Ví dụ 2. Cho tam giác ABC. Trên tia đối của AB lấy điểm D mà  AD = AB, trên tia đối

                     tia AC lấy điểm E mà AE = AC. Gọi M; N lần lượt là các điểm trên BC và ED

                      sao cho CM = EN.

                    Chứng minh ba điểm M; A; N thẳng hàng.

Gợi ý: Chứng minh  từ đó suy ra ba điểm M; A; N thẳng hàng.

BÀI GIẢI (Sơ lược)

          ABC = ADE (c.g.c)

          ACM = AEN (c.g.c)

          Mà  (vì ba điểm E; A; C thẳng hàng) nên

Vậy ba điểm M; A; N thẳng hàng (đpcm)

BÀI TẬP THỰC HÀNH CHO PHƯƠNG PHÁP 1

Bài 1: Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD = AC, trên tia đối

          của tia AC lấy điểm E sao cho AE = AB. Gọi M, N lần lượt là trung điểm của BE và

          CD.

          Chứng minh ba điểm M, A, N thẳng hàng.

Bài 2: Cho tam giác ABC vuông ở A có . Vẽ tia Cx  BC (tia Cx và điểm A ở

          phía ở cùng phía bờ BC), trên tia Cx lấy điểm E sao cho CE = CA. Trên tia đối của tia

          BC lấy điểm F sao cho BF = BA.

          Chứng minh ba điểm E, A, F thẳng hàng.

Bài 3: Cho tam giác ABC cân tại A, điểm D thuộc cạnh AB. Trên tia đối của tia CA lấy điểm

          E sao cho CE = BD. Kẻ DH và EK vuông góc với BC (H và K thuộc đường thẳng BC)

          Gọi M là trung điểm HK.

          Chứng minh ba điểm D, M, E thẳng hàng.

Bài 4: Gọi O là trung điểm của đoạn thẳng AB. Trên hai nửa mặt phẳng đối nhau bờ AB, kẻ

          Hai tia Ax và By sao cho .Trên Ax lấy hai điểm C và E(E nằm giữa A và C),

          trên By lấy hai điểm D và F ( F nằm giữa B và D) sao cho AC = BD, AE = BF.

          Chứng minh ba điểm C, O, D thẳng hàng , ba điểm E, O, F thẳng hàng.

Bài 5.Cho tam giác ABC . Qua A vẽ đường thẳng xy // BC. Từ điểm M trên cạnh BC, vẽ các

          đường thẳng song song AB và AC, các đường thẳng này cắt xy theo thứ tự tại D và E.

          Chứng minh các đường thẳng AM, BD, CE cùng đi qua một điểm.

                                                              PHƯƠNG PHÁP 2

    Ví dụ 1: Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của các cạnh AC, AB. Trên

                  Các đường thẳng BM và CN lần lượt lấy các điểm D và E sao cho M là trung  

                 điểm BD và N là trung điểm EC.

                  Chứng minh ba điểm E, A, D thẳng hàng.

Hướng dẫn: Xử dụng phương pháp 2                                            

                  Ta chứng minh AD // BC và AE // BC.

BÀI GIẢI.

                 BMC và DMA có:

                   MC = MA (do M là trung điểm AC)

                    (hai góc đối đỉnh)

                   MB = MD (do M là trung điểm BD)

                  Vậy: BMC = DMA (c.g.c)

                   Suy ra: , hai góc này ở vị trí so le trong nên BC // AD (1)

                   Chứng minh tương tự : BC // AE (2)

                   Điểm A ở ngoài BC có một và chỉ một đường thẳng song song BC nên từ (1)

                   và (2) và theo Tiên đề Ơ-Clit suy ra ba điểm E, A, D thẳng hàng. 

   Ví dụ 2: Cho hai đoạn thẳng  AC và BD cắt nhau tai trung điểm O của mỗi đoạn. Trên tia

                 AB lấy lấy điểm M sao cho B là trung điểm AM, trên tia AD lấy điểm N sao cho

                 D là trung điểm AN. 

1/ \(x^3+2=3\sqrt[3]{3x-2}\)

Đặt \(\sqrt[3]{3x-2}=a\) thì ta có hệ

\(\hept{\begin{cases}x^3+2-3a=0\\a^3+2-3x=0\end{cases}}\)

Lấy trên - dưới ta được

\(x^3-a^3+3x-3a=0\)

\(\Leftrightarrow\left(x-a\right)\left(x^2+ax+a^2+3\right)=0\)

\(\Leftrightarrow x=a\)

\(\Leftrightarrow x=\sqrt[3]{3x-2}\)

\(\Leftrightarrow x^3-3x+2=0\)

\(\Leftrightarrow\orbr{\begin{cases}x=1\\x=-2\end{cases}}\)

2/ \(x+\sqrt{5-x^2}+x\sqrt{5-x^2}=5\)

Đặt \(\sqrt{5-x^2}=a\ge0\) thì ta có hệ

\(\hept{\begin{cases}x+a+ax=5\\a^2+x^2=5\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}x+a+ax=5\\\left(a+x\right)^2-2ax=5\end{cases}}\)

Tới đây thì đơn giản rồi. Đặt \(\hept{\begin{cases}a+x=S\\ax=P\end{cases}}\) giải tiếp sẽ ra

\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{2}x-\dfrac{3}{5}>\dfrac{2}{5}\\\dfrac{1}{2}x-\dfrac{3}{5}< -\dfrac{2}{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{2}x>1\\\dfrac{1}{2}x< \dfrac{1}{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x>2\\x< \dfrac{2}{5}\end{matrix}\right.\)

24/12

24/12

7⁸¹ . 15²⁰¹⁸

7⁸¹\(\equiv\)( mod 10 )

7¹⁰\(\equiv\)9 ( mod 10 )

7⁸⁰\(\equiv\)1 ( mod 10 )

7⁸¹\(\equiv\)7 ( mod 10 )

Vậy chữ số tận cùng của 7⁸¹ là 1

15²⁰¹⁸\(\equiv\)( mod 10 )

15⁸\(\equiv\)5 ( mod 10 )

15⁸⁰\(\equiv\)5 ( mod 10 )

15⁹⁶⁰\(\equiv\)5 ( mod 10 )

15¹⁹²⁰\(\equiv\)5 ( mod 10 )

15²⁰⁰⁰\(\equiv\)5 ( mod 10 )

15²⁰⁰⁷\(\equiv\)5 ( mod 10 )

15²⁰¹⁴\(\equiv\)5 ( mod 10 ) 

15²⁰¹⁸\(\equiv\)5 ( mod 10 )

Vậy chữ số tận cùng của 15²⁰¹⁸ là 5

\(\Rightarrow\)Chữ số tận cùng của 7⁸¹ . 15²⁰¹⁸ là 7 . 5 = 35

Vậy chữ số tận cùng của 7⁸¹ . 15²⁰¹⁸ là 5

Hk tốt

a: =2/3+1/5*10/7

=2/3+2/7

=14/21+6/21=20/21

b: \(=\dfrac{1}{2}\cdot\dfrac{-3+2}{4}=\dfrac{1}{2}\cdot\dfrac{-1}{4}=\dfrac{-1}{8}\)

c: \(=\dfrac{3}{4}+\dfrac{9}{5}:\dfrac{3}{2}-1\)

=-1/4+9/5*2/3

=-1/4+18/15

=-1/4+6/5

=-5/20+24/20=19/20

d: \(=\dfrac{3}{2}\cdot\left(\dfrac{7}{3}-\dfrac{5}{3}\cdot4\right)\)

\(=\dfrac{7}{2}-\dfrac{5}{2}\cdot4=\dfrac{7}{2}-\dfrac{20}{2}=\dfrac{-13}{2}\)

1824 : 32 = 57

15 622 : 73 = 214

1824 : 32 = 57

15622 : 73 = 214

tick

Bn cần bài nào trong 2 bài nhỉ?

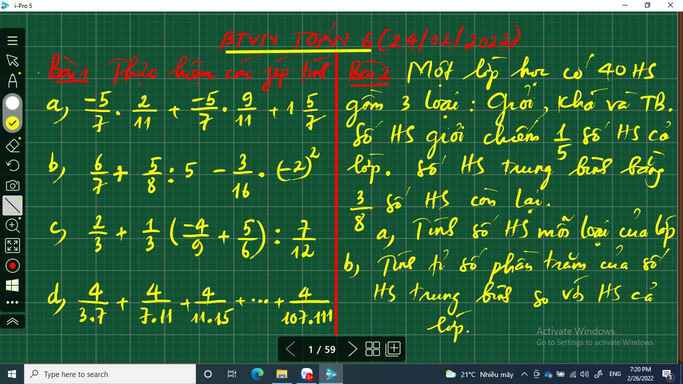
e tách câu hỏi ra nhe tạm thời cj giúp mụt câu nhe

a: \(=\dfrac{-5}{7}\left(\dfrac{2}{11}+\dfrac{9}{11}\right)+1+\dfrac{5}{7}=\dfrac{-5}{7}+1+\dfrac{5}{7}=1\)

b: \(=\dfrac{6}{7}+\dfrac{1}{8}-\dfrac{3}{16}\cdot4=\dfrac{6}{7}+\dfrac{1}{8}-\dfrac{3}{4}=\dfrac{13}{56}\)

c: \(=\dfrac{2}{3}+\dfrac{1}{3}\cdot\dfrac{-24+45}{54}\cdot\dfrac{12}{7}\)

\(=\dfrac{2}{3}+\dfrac{1}{3}\cdot\dfrac{21}{54}\cdot\dfrac{12}{7}=\dfrac{2}{3}+\dfrac{2}{9}=\dfrac{6+2}{9}=\dfrac{8}{9}\)

d: \(=\dfrac{1}{3}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{11}+...+\dfrac{1}{107}-\dfrac{1}{111}\)

\(=\dfrac{1}{3}-\dfrac{1}{111}=\dfrac{108}{333}=\dfrac{12}{37}\)