Tính chu vi và diện tích hìn tròn nội tiếp tam giác đều có cạnh a=12,46

Những câu hỏi liên quan
Tính diện tích hình tròn nội tiếp trong tam giác đều có cạnh a = 12,46 (cm).
Ta có: \(S_{ABC}=\frac{1}{2}.a.h_a=\frac{1}{2}a.a.\sin60^o=\frac{a^2\sqrt{3}}{4}\) khi ABC là tam giác đều.
Mà:\(S=p.r\Rightarrow r=\frac{S}{p}\) hay \(r=\frac{2S}{3a}=\frac{a\sqrt{3}}{6}=\frac{a}{2\sqrt{3}}\)
\(\Rightarrow r=\frac{a}{2\sqrt{3}}=\frac{12,46}{2\sqrt{3}}\)
Đúng 0
Bình luận (0)
a) Tính diện tích hình tròn nội tiếp tam giác đều có độ dài mỗi cạnh 3cm b) Tính diệntích hình tròn ngoại tiếp ngũ giác đều có độ dài mỗi cạnh 4dm
Viết chương trình con:
a) Tính chu vi và diện tích hình tròn theo bán kính.
b) Tính diện tích tam giác, bán kính đường tròn nội và ngoại tiếp tam giác theo 3 cạnh.
c) Tính thể tích và đường chéo hình hộp chữ nhật theo 3 kích thước.
Gọi a,b,c là số đo 3 cạnh của tam giác ABC , r là bán kính đường tròn nội tiếp tam giác . Tính diện tích tam giác theo p và r, trong đó p là nửa chu vi tam giác
Cho tam giác có 3 cạnh dài 9 cm,12 cm,15 cm.Tìm chu vi và diện tích của đường tròn nội tiếp của tam giác đó.
Cho nửa lục giác đều ABCD nội tiếp trong nửa đường tròn (O;R). Hai tiếp tuyến tại B và D cắt nhau ở T.
a) Chứng minh OT//AB
b) Chứng minh 3 điểm O, C, T thẳng hàng
c) Tính chu vi và diện tích tam giác TBD theo R
d) Tính theo R diện tích giới hạn bởi 2 cạnh TB, TD và cung BCD
Cho đường tròn (O;R). Viết công thức tính diện tích tam giác đều ngoại tiếp và diện tich tam giác đều nội tiếp (O;R). Áp dụng tính diện tích tam giác đều nội tiếp và tam giác đều ngoại tiếp khi R=1,123
Cho tam giác ABC có chu vi bằng 30cm và diện tích bằng 45cm2. Vẽ đường tròn (O) nội tiếp ΔABC. Tính bán kính của đường tròn đó.
Gọi D, E, F lần lượt là tiếp điểm của (O) với BC, AC, AB
\(\Rightarrow OD\perp BC\) ; \(OE\perp AC\) ; \(OF\perp AB\)
Và \(OD=OE=OF=R\)
Ta có:
\(S_{ABC}=S_{OAB}+S_{OAC}+S_{OBC}\)
\(=\dfrac{1}{2}OF.AB+\dfrac{1}{2}OE.AC+\dfrac{1}{2}OD.BC\)
\(=\dfrac{1}{2}R.AB+\dfrac{1}{2}R.AC+\dfrac{1}{2}R.BC\)
\(=\dfrac{1}{2}R.\left(AB+AC+BC\right)\)
\(\Rightarrow45=\dfrac{1}{2}R.30\)
\(\Rightarrow R=3\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng a và có đường cao h. Một hình trụ có các đường tròn đáy tiếp xúc với các cạnh của tam giác đáy được gọi là hình trụ nội tiếp trong lăng trụ. Hãy tính diện tích xung quanh của hình trụ nội tiếp đó.
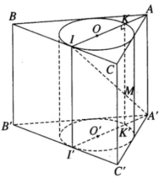
Hình trụ nội tiếp trong lăng trụ tam giác đều có đường tròn đáy tiếp xúc tại trung điểm các cạnh của tam giác đáy. Gọi I là trung điểm của cạnh BC, r là bán kính đáy của hình trụ nội tiếp trong lăng trụ
Ta có: 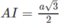
Do đó: 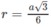
Ta có diện tích xung quanh của hình trụ nội tiếp lăng trụ là:
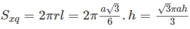
Đúng 0
Bình luận (0)














