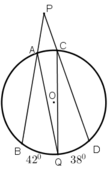
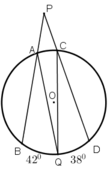
từ điểm P nằm ngoài đường trong O, kẻ hai đường cát tuyến PAB và PCD( A nằm giữa P và B,C nằm giữa P và D), các đường thẳng AD và BC cắt nhau tại Q. Chứng Minh P+AQC=2BCD

Những câu hỏi liên quan
Từ điểm P nằm ngoài đường tròn (O), kẻ hai cát tuyến PAB và PCD (A nằm giữa P và B, C nằm giữa P và D), các đường thẳng AD và BC cắt nhau tại Qa, Cho biết
P
^
60
0
và
A
Q
C
^
80...
Đọc tiếp
Từ điểm P nằm ngoài đường tròn (O), kẻ hai cát tuyến PAB và PCD (A nằm giữa P và B, C nằm giữa P và D), các đường thẳng AD và BC cắt nhau tại Q
a, Cho biết
P
^
=
60
0
và
A
Q
C
^
=
80
0
. Tính góc
B
C
D
^
b, Chứng minh PA.PB = PC.PD
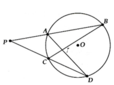
a, Ta có: B P D ^ = 1 2 s đ B D ⏜ - s đ A C ⏜ , A Q C ^ = 1 2 s đ B D ⏜ + s đ A C ⏜
=> B P D ^ + A Q C ^ = s đ B D ⏜ = 140 0
=> B C D ^ = 70 0
b, HS tự chứng minh
Đúng 0
Bình luận (0)
Bài 4: Từ điểm P nằm ngoài đường tròn (O), kẻ hai cát tuyến PAB và PCD (A nằm giữa P và B, C nằm giữa P và D), các đường thẳng AD và BC cắt nhau tại Q
a. Cho biết P = 60 độ và góc AQC = 80 độ tính góc BDC
b. Chứng minh: PA.PB = PC.PD
Từ điểm P nằm ngoài đường tròn O, kẻ 2 cát tuyến PAB và PCD (A nằm giữa P và B, C nẵm giữa P và D), các đường thẳng AD và BC cắt nhau tại Q
a) Cho biết góc P= 60 độ và góc AQC = 80 độ. Tính góc BCD
b) Chứng minh góc AED = góc PCD và góc BFC = góc PDC
Từ điểm P nằm ngoài đường tròn O, kẻ 2 cát tuyến PAB và PCD (A nằm giữa P và B, C nẵm giữa P và D), các đường thẳng AD và BC cắt nhau tại Q
a) Cho biết góc P= 60 độ và góc AQC = 80 độ. Tính góc BCD
b) Chứng minh góc AED = góc PCD và góc BFC = góc PDC
Từ điểm P nằm ngoài đường tròn O , kẻ hai cát tuyến PAB và PCD ( A nằm giữa P và B , C nằm giữa P và D ) các đường thẳng Ad và BC cắt nhau tại Q
a, Biết P = 60 độ , AQC = 80 độ . Tính BCD
b, Chứng minh : PA.PB=PC.PD
Lời giải:
a)
Ta có:
\(\widehat{P}=\frac{1}{2}(\text{cung BD-cung AC})=60^0(1)\)
\(\widehat{AQC}=\frac{1}{2}(\text{cung AC+cung BD)}=80^0(2)\)
Lấy \((1)+(2)\Rightarrow \text{cung BD}=60^0+80^0=140^0\)
Do đó \(\widehat{BCD}=\frac{1}{2}\text{cung BD}=70^0\)
b) Vì \(A,B,C,D\in (O)\) nên $ABCD$ là tứ giác nội tiếp.
\(\Rightarrow \widehat{PAC}=\widehat{PDB}\) (theo tính chất tgnt)
Xét tam giác $PAC$ và $PDB$ có:
\(\left\{\begin{matrix} \text{Chung}- \widehat{P}\\ \widehat{PAC}=\widehat{PDB}\end{matrix}\right.\Rightarrow \triangle PAC\sim \triangle PDB(g.g)\)
\(\Rightarrow \frac{PA}{PD}=\frac{PC}{PB}\Rightarrow PA.PB=PC.PD\) (đpcm)
Đúng 0
Bình luận (2)
Từ một điểm P ở ngoài đường tròn (O), kẻ cát tuyến PAB và PCD tới đường tròn. Gọi Q là một điểm nằm trên cung nhỏ BD (không chứa A và C) sao cho
sd
BQ
^
42
°
;
sd
QD
^
38
°
. Tính tổng
BPD
^
+
AQC...
Đọc tiếp
Từ một điểm P ở ngoài đường tròn (O), kẻ cát tuyến PAB và PCD tới đường tròn. Gọi Q là một điểm nằm trên cung nhỏ BD (không chứa A và C) sao cho sd BQ ^ = 42 ° ; sd QD ^ = 38 ° . Tính tổng BPD ^ + AQC ^
Từ một điểm P ở ngoài đường tròn (O), kẻ cát tuyến PAB và PCD tới đường tròn. Gọi Q là một điểm nằm trên cung nhỏ BD (không chứa A và C) sao cho
sd
BQ
^
42
°
;
sd
QD
^
38
°
. Tính tổng
BPD
^
+
AQC...
Đọc tiếp
Từ một điểm P ở ngoài đường tròn (O), kẻ cát tuyến PAB và PCD tới đường tròn. Gọi Q là một điểm nằm trên cung nhỏ BD (không chứa A và C) sao cho sd BQ ^ = 42 ° ; sd QD ^ = 38 ° . Tính tổng BPD ^ + AQC ^
Từ điểm P nằm ngoài đường tròn (O;R), Vẽ cát tuyến PAB không qua O (A nằm giữa P và B), từ A và B vẽ hai tiếp tuyến của (O) cắt nhau tại M. Hạ MH vuông góc với OP. a/ Giả sử OP=2R. Tính độ dài OH . B/ MH cắt (O) tại N (H nằm giữa M và N). chứng minh PN là tiếp tuyến của (O).
Từ điểm A ở ngoài đường tròn (O), kẻ hai tiếp tuyến AB, AC đến (O) với B, C là các tiếp điểm. Kẻ một đường thẳng d nằm giữa hai tia AB, AO và đi qua A cắt đường tròn (O) tại E, F (E nằm giữa A, F).1. Chứng minh bốn điểm A, B, O, C cùng thuộc một đường tròn.2. Gọi H là giao điểm của AD và BC. Chứng minh OH.OA OE^2.3. Đường thẳng qua O vuông góc với EF cắt BC tại E. Chứng minh SF là tiếp tuyến của đường tròn (O).4. Đường thẳng SF cắt các đường thẳng AB và AC tương ứng tại P và Q. Đường thẳng OF c...
Đọc tiếp
Từ điểm A ở ngoài đường tròn (O), kẻ hai tiếp tuyến AB, AC đến (O) với B, C là các tiếp điểm. Kẻ một đường thẳng d nằm giữa hai tia AB, AO và đi qua A cắt đường tròn (O) tại E, F (E nằm giữa A, F).
1. Chứng minh bốn điểm A, B, O, C cùng thuộc một đường tròn.2. Gọi H là giao điểm của AD và BC. Chứng minh OH.OA = OE^2.3. Đường thẳng qua O vuông góc với EF cắt BC tại E. Chứng minh SF là tiếp tuyến của đường tròn (O).4. Đường thẳng SF cắt các đường thẳng AB và AC tương ứng tại P và Q. Đường thẳng OF cắt BC tại K. Chứng minh rằng AK đi qua trung điểm của PQ.