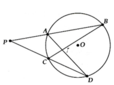
a, Ta có: B P D ^ = 1 2 s đ B D ⏜ - s đ A C ⏜ , A Q C ^ = 1 2 s đ B D ⏜ + s đ A C ⏜
=> B P D ^ + A Q C ^ = s đ B D ⏜ = 140 0
=> B C D ^ = 70 0
b, HS tự chứng minh

a, Ta có: B P D ^ = 1 2 s đ B D ⏜ - s đ A C ⏜ , A Q C ^ = 1 2 s đ B D ⏜ + s đ A C ⏜
=> B P D ^ + A Q C ^ = s đ B D ⏜ = 140 0
=> B C D ^ = 70 0
b, HS tự chứng minh
Từ điểm P nằm ngoài đường tròn O, kẻ 2 cát tuyến PAB và PCD (A nằm giữa P và B, C nẵm giữa P và D), các đường thẳng AD và BC cắt nhau tại Q
a) Cho biết góc P= 60 độ và góc AQC = 80 độ. Tính góc BCD
b) Chứng minh góc AED = góc PCD và góc BFC = góc PDC
Từ điểm P nằm ngoài đường tròn O, kẻ 2 cát tuyến PAB và PCD (A nằm giữa P và B, C nẵm giữa P và D), các đường thẳng AD và BC cắt nhau tại Q
a) Cho biết góc P= 60 độ và góc AQC = 80 độ. Tính góc BCD
b) Chứng minh góc AED = góc PCD và góc BFC = góc PDC
Cho đường tròn tâm O và điểm A nằm ngoài đường tròn. Một cát tuyến qua A cắt đường tròn (O) tại B và C (B nằm giữa A và C). Các tiếp tuyến của (O) tại B và C cắt nhau tại D. Đường thẳng qua D vuông góc với OA cắt (O) tại E và F (E nằm giữa D và F). Gọi M là giao điểm của DO và BC. Chứng minh
a,DC2=DE.DF
b, EMOF nội tiếp 1 đường tròn
c, AE là tiếp tuyến của (O)
Cho điểm A nằm ngoài đường tròn (O,R). Vẽ AB, AC là các tiếp tuyến của đường tròn (O) (B, C là các tiếp điểm). Vẽ cát tuyến ADE của đường tròn O ( D nằm giữa A và E). Các tiếp tuyến tại D và E của (O) cắt nhau tại K, OA cắt Bc tại H.
a) Chứng minh KH vuông góc với OA; K, B, C thẳng hàng.
b) AO cắt (O) tại M, N ( M nằm giữa O, H). Chứng minh KH, DN, EM đồng quy
Cho điểm A nằm ngoài đường tròn (O).Từ A kẻ hai tiếp tuyến AB,AC và cát tuyến ADE tới đường tròn (B,C là hai tiếp điểm;D nằm giữa A&E).Gọi H là giao điểm của AO và BC
a,Chứng minh rằng :ABOC là tứ giác nội tiếp
b,Chứng minh rằng :AH.AO=AD.AE
c,Tiếp tuyến tại D của đường tròn (O)cắt AB,AC theo thứ tự tại I và K.Qua điểm O kẻ đường thẳng vuông góc với OA cắt tia AB tại P và cắt tia AC tại Q.Chứng minh rằng IP+KQ>=PQ
Từ một điểm M nằm ngoài đường tròn (O) kẻ các tiếp tuyến MA,MB với đường tròn (A,B là các tiếp điểm). Một cát tuyến qua M, cắt (O) tại hai điểm C và D ( C nằm giữa M và D).
a) Chứng minh: AC.DB=AD.CB
b) Phân giác CAD cắt CD tại I. Chứng minh BI là phân giác góc CBD.
Cho đường tròn tâm O bán kính r. Gọi M là điểm bất kì nằm ngoài đường tròn tâm O kẻ cát tuyến bất kì MAB với (0) ( A nằm giữ M và B). Kẻ đường kính BC. Đường MC cắt (0) tại điểm thứ hai là D ( C nằm giữa M và D). Gọi N là giao điểm của AC và BD
a) CMR: BACD là tứ giác nội tiếp và góc AMC = DNC
b) CMR: BC vuông góc MN tại H
c) CMR: DCHN là tứ giác nội tiếp rồi chứng minh: MC .MD + NA .NC = MN2
d) Cho biết góc DNC = 450 Tính diện tích viên phân chắn cung AD theo R
cho đường tròn tâm O và điểm A nằm ngoài đường tròn.một cát tuyến qua A cắt đường tròn (O) tại B và C( B nằm giữa A và C) các tiếp tuyến của (O) tại B và C cắt nhau tại D Đường thẳng D vuông góc với OA cắt (O) tại E và F( E nằm giưa D và F ) gọi M là giao điểm của DO và và BC
Từ một điểm A nằm ngoài đường tròn (O) kẻ hai tiếp tuyến AB và AC đến (O) (B và C là các tiếp điểm) và một cát tuyến ADE không đi qua tâm O (D nằm giữa A và E), gọi I là trung điểm của DE.
a) Chứng minh 5 điểm A;B;O;I;C cùng nằm trên một đường tròn suy ra IA là phân giác của góc BIC
b) BC cắt AE tại K. Chứng minh KA.KI=KD.KE
c) Qua C kẻ đường thẳng song với AB, đường này cắt các đướng thẳng BE, BD lần lượt tại P và Q. Chứng minh C là trung điểm của PQ.
giai dum minh cau c