Cho tam giác ABC trên AC lấy điểm M sao cho MA = MD;trên BM lấy điểm I sao cho B = 2 x MY nối AC kéo dài cắt BC tại H. So sánh HB với HC.

Những câu hỏi liên quan
cho tam giác ABC (AB>AC). Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MA=MD. a) Chứng minh tam giác ACM= tam giác DBM. b) Kẻ BE vuông góc với AM tại E. Trên tia MD lấy điểm F sao cho M là trung điểm của EF. Chứng minh CF vuông góc với AD. c) Trên tia FB lấy điểm G sao cho B là trung điểm FG. Gọi H là trung điểm của BE. Chứng minh ba điểm G,H,C thẳng hàng
a: Xét ΔMAC và ΔMDB có
MA=MD
\(\widehat{AMC}=\widehat{DMB}\)(hai góc đối đỉnh)
MC=MB
Do đó: ΔMAC=ΔMDB
b: Xét ΔMEB và ΔMFC có
ME=MF
\(\widehat{BME}=\widehat{CMF}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMEB=ΔMFC
=>\(\widehat{MEB}=\widehat{MFC}\)
=>\(\widehat{MFC}=90^0\)
=>CF\(\perp\)AD
c: Xét tứ giác BFCE có
M là trung điểm chung của BC và FE
=>BFCE là hình bình hành
=>BF//CE và BF=CE
Ta có: BF//CE
B\(\in\)FG
Do đó: BG//CE
Ta có: BF=CE
BF=BG
Do đó: BG=CE
Xét tứ giác BGEC có
BG//EC
BG=EC
Do đó: BGEC là hình bình hành
=>BE cắt GC tại trung điểm của mỗi đường
mà H là trung điểm của BE
nên H là trung điểm của GC
=>G,H,C thẳng hàng
Đúng 1
Bình luận (0)
Cho tam giác AbC có ab=ac M là trung điểm của BC trên tia đối của tia MA lấy điểm D sao cho am=mb chứng minh rằng a/ tam giác Abc=Amc B/ trên tia đối của tia ma lấy điểm D sao cho am=md ,CM, tam giác mba=mcd
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
b: Xét ΔMBA và ΔMCD có
MB=MC
\(\widehat{AMB}=\widehat{DMC}\)
MA=MD
Do đó: ΔMBA=ΔMCD
Đúng 1
Bình luận (0)
cho tam giác ABC vuông tại A có AB=6cm BC=10cm gọi M là trung điểm BC trên tia đối MA lấy D sao cho MD=MA
a.tính AC, tính ABD
b.chứng minh tam giác AMB = tam giác DMC, tam giác ABC = tam giác BAD
c.trên cạch AC lấy E, trên BD lấy F sao cho AE=DF chứng minh E M F thẳng hàng
d, so sánh AM và BC
a: AC=8cm
Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
Suy ra: \(\widehat{ABD}=90^0\)
b: Xét ΔAMB và ΔDMC có
MA=MD
MB=MC
AB=DC
Do đó: ΔAMB=ΔDMC
Xét ΔABC và ΔBAD có
BA chung
BC=AD
AC=BD
Do đó: ΔABC=ΔBAD
c: Xét tứ giác AEDF có
AE//DF
AE=DF
Do đó AEDF là hình bình hành
Suy ra: HAi đường chéo AD và EF cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của AD
nên M là trung điểm của FE
hay F,M,E thẳng hàng
Đúng 0
Bình luận (0)
1)tam giác ABC nhọn, trên tia đối AB lấy D sao cho AB=AD, trên tia đối AC lấy điểm M sao cho AC=AM . Tứ giác BCDM là hình j ? why ? 2) Cho tam giác ABC vuông tại A , biết AB=3cm, AC=4cm a) Tính AC b) Gọi M là trung điểm của BC, trên tia đối của MA lấy D sao cho MA=MD. Tứ giác ABCD là hình j ? why ?
Cho tam giác ABC, M là trung điểm BC .Trên tia đối của tia MA lấy điểm D sao cho MD=MA. C/m
a) Tam giác AMB = tam giác DMC
b) CD//AB
c) Trên cạnh AB lấy điểm E, trên cạnh DC lấy điểm F sao cho AE=DF. C/m ba điểm E,M,F thẳng hàng
b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: CD//AB
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB < AC. Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA
b. Chứng minh AC > CD
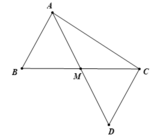
b. Vì ΔABM = ΔBCM ⇒ AB = DC mà AB < AC ⇒ CD < AC (2 điểm)
Đúng 0
Bình luận (0)
1. Cho tam giác ABC ( AB<AC ). M là trung điểm của BC, trên tia đối của MA lấy D sao cho MA=MD. Chứng minh:
a) Tam giác ABM = tam giác DCM
b) AC//BD
c)Trên nửa mặt phẳng bờ AD không chứa B, vẽ tia Ax//CD. Trên Ax lấy điểm H sao cho AH=BC. Chứng minh 3 điểm : H;C;D thẳng hàng
Cho tam giác ABC vuông tại A. Điểm M là trung điểm của cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho MA = MD. Chứng minh rằng: a) Tam giác AMC = tam giác DMB b) AC = BD.
a: Xét ΔAMC và ΔDMB có
MA=MD
\(\widehat{AMC}=\widehat{DMB}\)
MC=MB
Do đó: ΔAMC=ΔDMB
Đúng 0
Bình luận (0)
Cho tam giác ABC, M là trung điểm BC. Trên tia đối MA lấy điểm D sao cho MA=MD. Chứng minh rằng AB=CD, AC=BD
Xét \(\Delta ABM\) và \(\Delta DCM\) có
AM = DM (gt)
\(\widehat{AMB}=\widehat{DMC}\) (đối đỉnh_
BM = CM (gt)
=> \(\Delta ABM\) = \(\Delta DCM\) (c.g.c)
=> AB = DC ( 2 cạnh t/ứ)
Xét \(\Delta ACM\) và \(\Delta DBM\) có
AM = DM (gt)
\(\widehat{AMC}=\widehat{BMD}\) (đối đỉnh)
CM = BM (gt)
=> \(\Delta ACM\) = \(\Delta DBM\) (c.g.c)
=> AC = DB ( 2 cạnh t/ứ)














