So sánh phân số 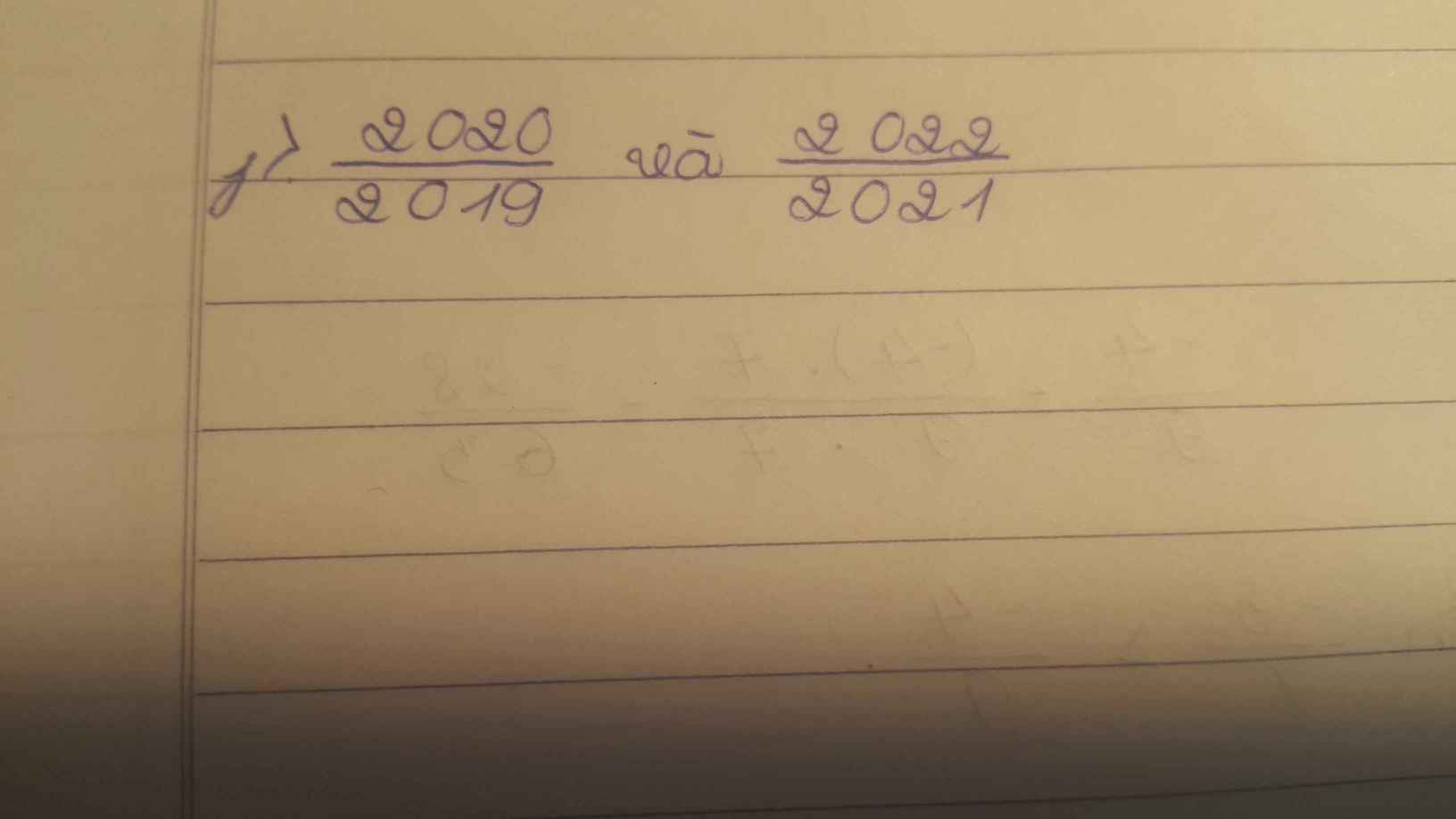

Những câu hỏi liên quan
So sánh hai phân số có cùng tử số (theo mẫu)*Nhớ lại: Trong hai phân số có cùng tử số, phân số nào có mẫu số bé hơn thì phân số đó lớn hơn.Mẫu: So sánh: b) So sánh:
Đọc tiếp
So sánh hai phân số có cùng tử số (theo mẫu)
*Nhớ lại: Trong hai phân số có cùng tử số, phân số nào có mẫu số bé hơn thì phân số đó lớn hơn.
Mẫu: So sánh: 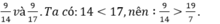
b) So sánh: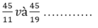
*Nhớ lại: Trong hai phân số có cùng tử số, phân số nào có mẫu số bé hơn thì phân số đó lớn hơn.
Mẫu: So sánh: 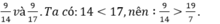
b) So sánh: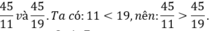
Đúng 0
Bình luận (0)
Ta có 11 < 19, nên : \(\frac{9}{14}\)> \(\frac{55}{9}\)
So sánh hai phân số có cùng tử số (theo mẫu)*Nhớ lại: Trong hai phân số có cùng tử số, phân số nào có mẫu số bé hơn thì phân số đó lớn hơn.Mẫu: So sánh: a) So sánh:
Đọc tiếp
So sánh hai phân số có cùng tử số (theo mẫu)
*Nhớ lại: Trong hai phân số có cùng tử số, phân số nào có mẫu số bé hơn thì phân số đó lớn hơn.
Mẫu: So sánh: 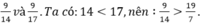
a) So sánh: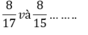
*Nhớ lại: Trong hai phân số có cùng tử số, phân số nào có mẫu số bé hơn thì phân số đó lớn hơn.
Mẫu: So sánh: 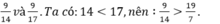
a) So sánh: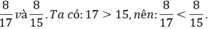
Đúng 1
Bình luận (0)
ooooooooooooooooooooo
SO SÁNH PHÂN SỐ
Bài 1: Không quy đồng mẫu hãy so sánh phân số sau bằng cách nhanh nhất:
a) và b) và
Bài 2. So sánh các phân số sau ; ;
Đọc tiếp
SO SÁNH PHÂN SỐ
Bài 1: Không quy đồng mẫu hãy so sánh phân số sau bằng cách nhanh nhất:
a) và
b)
và
Bài 2. So sánh các phân số sau ;
;
a) ta có: \(1-\frac{2012}{2013}=\frac{1}{2013}\)
\(1-\frac{2013}{2014}=\frac{1}{2014}\)
mà \(\frac{1}{2013}>\frac{1}{2014}\) nên \(\frac{2013}{2014}>\frac{2012}{2013}\)
sao giống lớp 4 thế ta
hãy khoanh vào câu trả lời đúng
1 nêu cách so sánh hợp lý nhất để so sánh 2 phân số 4/3 và 18/19
A. so sánh tử số
B. so sánh mẫu số
C. so sánh quy đồng
D. so sánh với 1
E. so sánh phân số trung gian
Đáp án là D nha bạn. Vì 4/3 lớn hơn 1 mà 18/19 lại nhỏ hơn 1!
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
So sánh các phân số sau bằng cách quy đồng tử số : 2/5 , 4/2, 6/2,9/4,5/4.
a. So sánh các số từ bé đến lớn , so sánh các số từ lớn đến bé .
b. Sau khi so sánh các số , ta rút gọn phân số lớn nhất và phân số bé nhất
Ta có:
\(\frac{2}{5}=\frac{8}{20};\frac{4}{2}=\frac{40}{20};\frac{6}{2}=\frac{60}{20};\frac{9}{4}=\frac{45}{20};\frac{5}{4}=\frac{25}{20}\)
Vì \(\frac{8}{20}
Đúng 0
Bình luận (0)
8/20 nhaaaaaaaaaaa
Xem thêm câu trả lời
Khi nào ta có thể so sánh hai phân số bằng phương pháp so sánh với phân số trung gian? A. Khi tử số của phân số thứ nhất bé hơn tử số của phân số thứ hai và mẫu số của phân số thứ nhất lại lớn hơn mẫu số của phân số thứ hai B. Khi tử số của phân số thứ nhất lớn hơn tử số của phân số thứ hai và mẫu số của phân số thứ nhất lại nhỏ hơn mẫu của phân số thứ hai. C. Cả A và B đều sai D. Cả A và B đều đúng
Đọc tiếp
Khi nào ta có thể so sánh hai phân số bằng phương pháp so sánh với phân số trung gian?
A. Khi tử số của phân số thứ nhất bé hơn tử số của phân số thứ hai và mẫu số của phân số thứ nhất lại lớn hơn mẫu số của phân số thứ hai
B. Khi tử số của phân số thứ nhất lớn hơn tử số của phân số thứ hai và mẫu số của phân số thứ nhất lại nhỏ hơn mẫu của phân số thứ hai.
C. Cả A và B đều sai
D. Cả A và B đều đúng
Khi tử số của phân số thứ nhất bé hơn tử số của phân số thứ hai và mẫu số của phân số thứ nhất lại lớn hơn mẫu số của phân số thứ hai hoặc khi tử số của phân số thứ nhất lớn hơn tử số của phân số thứ hai và mẫu số của phân số thứ nhất lại nhỏ hơn mẫu số của phân số thứ hai thì ta có thể so sánh hai phân số bằng phương pháp so sánh với phân số trung gian.
Do đó cả hai đáp án A và B đều đúng
Đáp án cần chọn là D
Đúng 0
Bình luận (0)
Khi nào ta có thể so sánh hai phân số bằng phương pháp so sánh với phân số trung gian? A. Khi tử số của phân số thứ nhất bé hơn tử số của phân số thứ hai và mẫu số của phân số thứ nhất lại lớn hơn mẫu số của phân số thứ hai B. Khi tử số của phân số thứ nhất lơn hơn tử số của phân số thứ hai và mẫu số của phân số thứ nhất lại nhỏ hơn mẫu số của phân số thứ hai C. Cả A và B đều sai D. Cả A và B đều đúng
Đọc tiếp
Khi nào ta có thể so sánh hai phân số bằng phương pháp so sánh với phân số trung gian?
A. Khi tử số của phân số thứ nhất bé hơn tử số của phân số thứ hai và mẫu số của phân số thứ nhất lại lớn hơn mẫu số của phân số thứ hai
B. Khi tử số của phân số thứ nhất lơn hơn tử số của phân số thứ hai và mẫu số của phân số thứ nhất lại nhỏ hơn mẫu số của phân số thứ hai
C. Cả A và B đều sai
D. Cả A và B đều đúng
Khi tử số của phân số thứ nhất bé hơn tử số của phân số thứ hai và mẫu số của phân số thứ nhất lại lớn hơn mẫu số của phân số thứ hai hoặc khi tử số của phân số thứ nhất lớn hơn tử số của phân số thứ hai và mẫu số của phân số thứ nhất lại nhỏ hơn mẫu số của phân số thứ hai thì ta có thể so sánh hai phân số bằng phương pháp so sánh với phân số trung gian.
Do đó cả hai đáp án A và B đều đúng.
Đáp án D.
Đúng 0
Bình luận (0)
so sánh hai phân số có cùng tử số phân số nào có mẫu số bé hơn thì phân số đó lớn hơn * nhớ lại trong hai phân số có cùng tử số , phân số nào có mẫu số bé thì phân số đó lớn hơn .mẫu ; so sánh 9 / 14 và 9 / 17 . ta có ; 14 17 , nên ; 9 / 14 9 /17a ) so sánh ; 8 / 17 và 8 / 15 ............................................................................b ) so sánh ; 45 / 11 và 45 / 19 .......................................................................
Đọc tiếp
so sánh hai phân số có cùng tử số phân số nào có mẫu số bé hơn thì phân số đó lớn hơn
* nhớ lại trong hai phân số có cùng tử số , phân số nào có mẫu số bé thì phân số đó lớn hơn .
mẫu ; so sánh 9 / 14 và 9 / 17 . ta có ; 14 < 17 , nên ; 9 / 14 > 9 /17
a ) so sánh ; 8 / 17 và 8 / 15 ............................................................................
b ) so sánh ; 45 / 11 và 45 / 19 .......................................................................
a) Ta có 15<17 nên 8/17<8/15
b)ta có 11<19 nên 45/11>45/19
Đúng 0
Bình luận (0)
so sánh 2 phân số
17/40 và 18/37
(Gợi ý : Lấy 1 phân số trung gian để so sánh 2 phân số kia)
Ta có : 17/40 < 17/37 <18/37
Suy ra 17/40 < 18/37
a) So sánh hai số thập phân sau: -0,617 và -0,614.
b) Nêu quy tắc so sánh 2 số thập phân hữu hạn.
a) Vì 0,617 > 0,614 nên -0,617 < -0,614
b) * So sánh 2 số thập phân khác dấu: Số thập phân âm luôn nhỏ hơn số thập phân dương
* So sánh 2 số thập phân dương:
Bước 1: So sánh phần số nguyên của 2 số thập phân đó. Số thập phân nào có phần số nguyên lớn hơn thì lớn hơn
Bước 2: Nếu 2 số thập phân dương đó có phần số nguyên bằng nhau thì ta tiếp tục so sánh từng cặp chữ số ở cùng một hàng( sau dấu ","), kể từ trái sang phải cho đến khi xuất hiện cặp chữ số đầu tiên khác nhau. Ở cặp chữ số khác nhau đó, chữ số nào lớn hơn thì số thập phân chứa chữ số đó lớn hơn
*So sánh 2 số thập phân âm:
Nếu a < b thì –a > - b
Đúng 0
Bình luận (0)
a: -0,617<-0,614
b: Chúng ta sẽ so sánh phần nguyên trước. nếu phần nguyên bên nào lớn hơn thì bên đó lớn hơn. Nếu phần nguyên bằng nhau thì sẽ so đến phần thập phân với quy tắc tương tự theo chiều từ trái qua phải, chừng nào tìm được hai số ở cùng vị trí mà số này lớn hơn số kia thì kết luận số đó lớn hơn
Đúng 0
Bình luận (0)
























