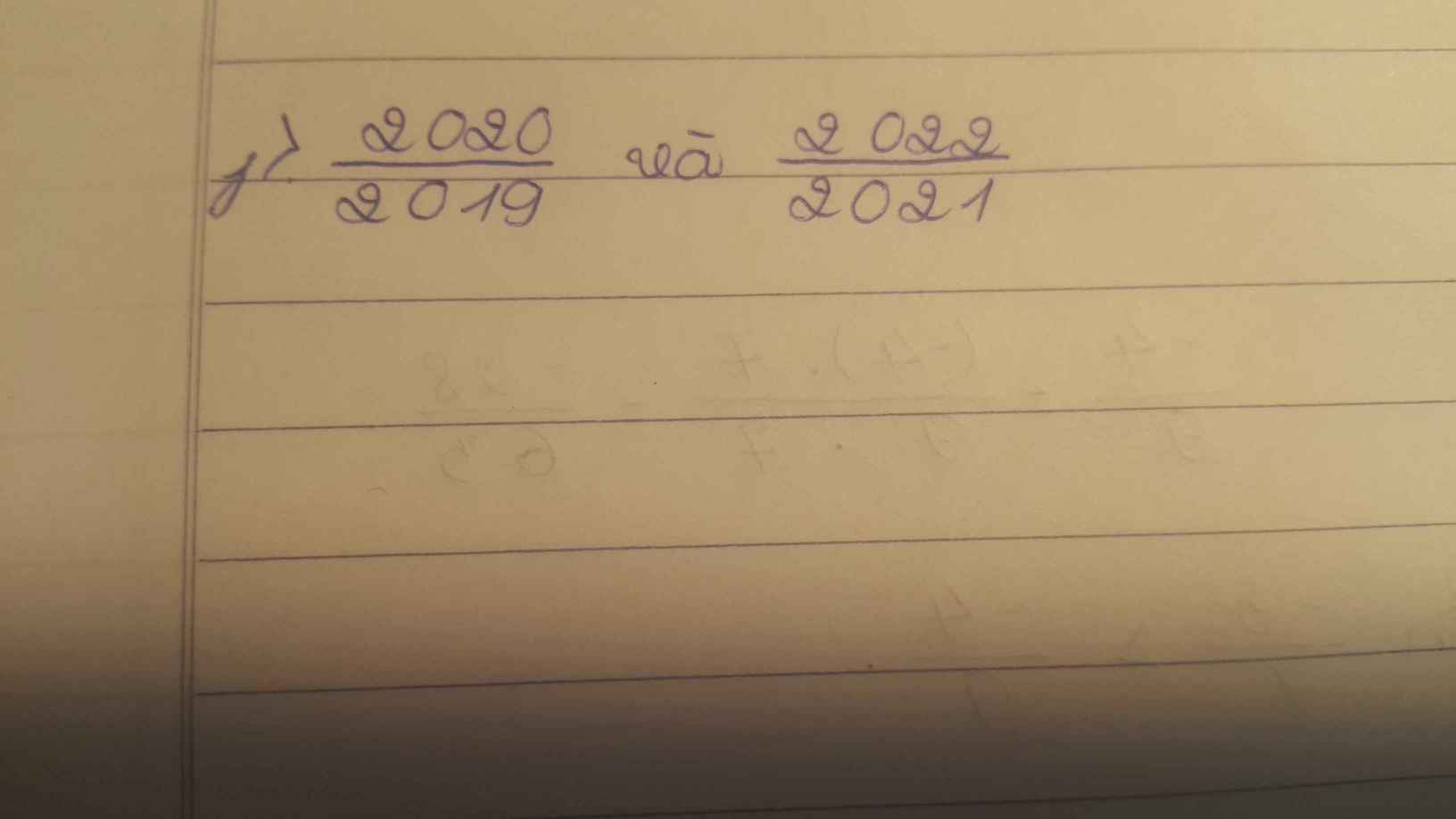\(\dfrac{2020}{2019}=\dfrac{2019+1}{2019}=\dfrac{2019}{2019}+\dfrac{1}{2019}=1+\dfrac{1}{2019}\) ;
\(\dfrac{2022}{2021}=\dfrac{2021+1}{2021}=\dfrac{2021}{2021}+\dfrac{1}{2021}=1+\dfrac{1}{2021}\);
Vì \(2019< 2021\) ⇒ \(\dfrac{1}{2019}>\dfrac{1}{2021}\) ⇒\(1+\dfrac{1}{2019}>1+\dfrac{1}{2021}\) ⇒\(\dfrac{2020}{2019}>\dfrac{2022}{2021}\)
\(\dfrac{2020}{2019}>1\)
\(\dfrac{2022}{2021}< 1\)
\(\Rightarrow\dfrac{2019}{2020}>\dfrac{2022}{2021}\)