Giúp m bài này với mn ơi mình đang cần gấp

Những câu hỏi liên quan
Mn ơi giúp mình bài này với mình đang cần gấp ko cần dịch đâu ạ
1 think
2 that
3 said
4 that
5 that
6 tell
7 that
8 that
9 that
10 that
11 think
12 assurance
13 that
14 That
15 That
Đúng 1
Bình luận (0)
Giúp mình bài này với mn ơi mình đang cần gấp
Tính theo cách hợp lí
67.12+67.89-67
$67\cdot12+67\cdot89-67$
$=67\cdot(12+89-1)$
$=67\cdot(101-1)$
$=67\cdot100$
$=6700$
Đúng 2
Bình luận (0)
Mn ơi mn giúp mk bài này vs ạ (mình đang cần gấp🥺🥺🥺). Thanks mn.
Giúp em bài này với mn ơi em đang cần gấp
Mn ơi giúp em bài này với en đang cần gấp😢
mn ơi giúp mình bài này với mình cần gấp ! 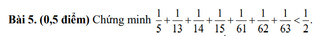
mn ơi giúp mình bài này với mình cần gấp ! 
Gọi số học sinh khối 6 là x
Theo đề, ta có: \(x-3\in BC\left(8;12;15\right)\)
\(\Leftrightarrow x-3\in\left\{120;240;360;...\right\}\)
\(\Leftrightarrow x\in\left\{123;243;363\right\}\)
mà 200<=x<=300
nên x=243
Đúng 1
Bình luận (0)
Gọi số học sinh khối 6 là a
a + 3 \(⋮8;12;15\)
\(\Rightarrow\) \(a+3\in BC\left(8;12;15\right)\)
8 = 2 . 3
12 = 22 . 3
15 = 3 . 5
\(\Rightarrow\) BCNN (8; 12; 15) = 22 . 3 . 5 = 60
Mà 203 < a + 3 < 303 học sinh
\(\Rightarrow\) a + 3 \(\in\) {240; 300}
\(\Rightarrow\) a \(\in\) {237; 207}
Đúng 1
Bình luận (1)

mn ơi, giúp mình với mình cần rất gấp bài này
Bài 9:
a: Xét ΔAMD vuông tại M và ΔAMI vuông tại M có
AM chung
MD=MI
Do đó: ΔAMD=ΔAMI
Xét ΔAND vuông tại N và ΔANK vuông tại N có
AN chung
ND=NK
Do đó: ΔAND=ΔANK
b: ta có: ΔAMD=ΔAMI
=>\(\widehat{MAD}=\widehat{MAI}\)
=>\(\widehat{DAB}=\widehat{IAB}\)
mà tia AB nằm giữa hai tia AD,AI
nên AB là phân giác của góc DAI
=>\(\widehat{DAI}=2\cdot\widehat{DAB}\)
Ta có: ΔAND=ΔANK
=>\(\widehat{DAN}=\widehat{KAN}\)
=>\(\widehat{DAC}=\widehat{KAC}\)
mà tia AC nằm giữa hai tia AD,AK
nên AC là phân giác của góc DAK
=>\(\widehat{DAK}=2\cdot\widehat{DAC}\)
Ta có: \(\widehat{DAK}+\widehat{DAI}=\widehat{KAI}\)
=>\(\widehat{KAI}=2\cdot\left(\widehat{DAB}+\widehat{DAC}\right)\)
=>\(\widehat{KAI}=2\cdot\widehat{BAC}=180^0\)
=>K,A,I thẳng hàng
c: Ta có: AD=AI(ΔADM=ΔAIM)
AD=AK(ΔADN=ΔAKN)
Do đó: AI=AK
mà K,A,I thẳng hàng
nên A là trung điểm của KI
d: Xét tứ giác AMDN có
\(\widehat{AMD}=\widehat{AND}=\widehat{MAN}=90^0\)
=>AMDN là hình chữ nhật
Hình chữ nhật AMDN có AD là phân giác của góc MAN
nên AMDN là hình vuông
=>DA là phân giác của góc NDM
=>DA là phân giác của góc KDI
Xét ΔDKI có
DA là đường trung tuyến
DA là đường phân giác
Do đó: ΔDKI cân tại D
Ta có: ΔDKI cân tại D
mà DA là đường trung tuyến
nên DA\(\perp\)KI
Đúng 0
Bình luận (0)
Mn ơi giải giúp mình bài hình này nhé khoảng tầm 22h mình quay lại lấy nha mai đi học r mình đang cần gấp cảm ơn mn 
a) Xét ΔOBH và ΔODA có
OB=OD(gt)
\(\widehat{BOH}=\widehat{DOA}\)(hai góc đối đỉnh)
OH=OA(O là trung điểm của HA)
Do đó: ΔOBH=ΔODA(c-g-c)
Suy ra: \(\widehat{OHB}=\widehat{OAD}\)(hai góc tương ứng)
mà \(\widehat{OHB}=90^0\)(gt)
nên \(\widehat{OAD}=90^0\)
hay AH\(\perp\)AD(đpcm)
b) Xét ΔAOE vuông tại A và ΔHOC vuông tại H có
OA=OH(O là trung điểm của AH)
\(\widehat{AOE}=\widehat{HOC}\)(hai góc đối đỉnh)
Do đó: ΔAOE=ΔHOC(Cạnh góc vuông-góc nhọn kề)
Suy ra: AE=HC(hai cạnh tương ứng)(1)
Ta có: ΔAOD=ΔHOB(cmt)
nên AD=HB(Hai cạnh tương ứng)(2)
Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔAHB=ΔAHC(Cạnh huyền-cạnh góc vuông)
Suy ra: HB=HC(Hai cạnh tương ứng)(3)
Từ (1), (2) và (3) suy ra AD=AE
mà E,A,D thẳng hàng(gt)
nên A là trung điểm của DE
Đúng 1
Bình luận (0)
) Xét ΔOBH và ΔODA có
OB=OD(gt)
ˆBOH=ˆDOABOH^=DOA^(hai góc đối đỉnh)
OH=OA(O là trung điểm của HA)
Do đó: ΔOBH=ΔODA(c-g-c)
Suy ra: ˆOHB=ˆOADOHB^=OAD^(hai góc tương ứng)
mà ˆOHB=900OHB^=900(gt)
nên ˆOAD=900OAD^=900
hay AH⊥⊥AD(đpcm)
b) Xét ΔAOE vuông tại A và ΔHOC vuông tại H có
OA=OH(O là trung điểm của AH)
ˆAOE=ˆHOCAOE^=HOC^(hai góc đối đỉnh)
Do đó: ΔAOE=ΔHOC(Cạnh góc vuông-góc nhọn kề)
Suy ra: AE=HC(hai cạnh tương ứng)(1)
Ta có: ΔAOD=ΔHOB(cmt)
nên AD=HB(Hai cạnh tương ứng)(2)
Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔAHB=ΔAHC(Cạnh huyền-cạnh góc vuông)
Suy ra: HB=HC(Hai cạnh tương ứng)(3)
Từ (1), (2) và (3) suy ra AD=AE
mà E,A,D thẳng hàng(gt)
nên A là trung điểm của DE
Đúng 0
Bình luận (0)