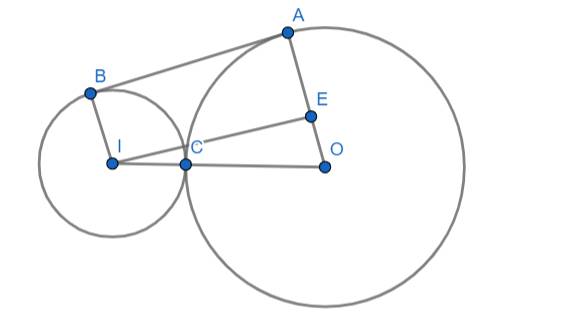
Do AB là tiếp tuyến chung của (O) và (I) nên: 

\(\left\{{}\begin{matrix}\widehat{IBA}=90^o\\\widehat{OAB}=90^o\end{matrix}\right.\) (tiếp tuyến vuông góc với bán kính) 

\(\Rightarrow\left\{{}\begin{matrix}IB\perp AB\\OA\perp AB\end{matrix}\right.\)

\(\Rightarrow IB//OA\) (cùng vuông góc với AB) 

\(\Rightarrow ABOI\) là hình thang 

Ta kẻ IE vuông góc với OA tại E 

⇒ IEAB là hình chữ nhật 

⇒ \(IB=AE=2\left(cm\right)\) (cặp cạnh đối của hình chữ nhật) 

\(\Rightarrow OE=OA-AE=8-2=6\left(cm\right)\) 

Mà: \(OI=OC+IC=2+8=10\left(cm\right)\) 

Xét ΔIEO vuông tại E áp dụng định lý Py-ta-go ta có: 

\(IO^2=OE^2+IE^2\)

\(\Leftrightarrow10^2=6^2+IE^2\)

\(\Leftrightarrow IE=\sqrt{100-36}=\sqrt{64}\)

\(\Leftrightarrow IE=8\left(cm\right)\)

Mà: \(AB=IE=8\left(cm\right)\) (ABIE là hình chữ nhật) 

Diện tích của tứ giác ABOI có AB là đường cao là:

\(S_{ABOI}=\dfrac{\left(IB+OA\right)\cdot AB}{2}=\dfrac{\left(2+8\right)\cdot8}{2}=40\left(cm^2\right)\)

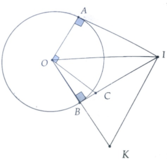
a, Chứng minh C là trực tâm của tam giác OIK. Từ đó suy ra KC ⊥ OI tại H

b, IA=12cm

Chứng minh ΔKOI cân tại K

Đặt  KO = KI = x (x>0)

Có  I K 2 = I B 2 + B K 2

Hay x 2 = 12 2 + x - 9 2

=> x = 12,5 => IK = 12,5cm

OB=căn18

b>  Xét 2 tam giác bằng nhau đó là tam giác OAB=BCO là ra 2 góc cần xét 

ta có tam giác AOC cân và OH là đường cao nên cũng là đường phân giác =>OAH=HOC

xét 2 tam giác OAB và tam giÁC BCO có OA=OB (bán kính )AOH=HOC(cmt) OB CHUNG => AOB=BCO(C-G-C)=>GÓC OAB=BCO hay OC vuông BC=>...............

AC=3