Những câu hỏi liên quan
cho tam giác ABC Cân tại A có AB=5cm, BC=4cm . Vẽ AH vuông góc BC tại H
a)CM:tam giác AHB=tam giác AHC và H là trung điểm của BC
b)Tính HB và AH
c)Gọi D là trung điểm của AC.CM tam giác ADH là tam giác cân
6 tháng 1 2021 lúc 19:40
Tam giác ABC cân tại A., AH \(\perp\) BC (H thuộc BC).
a/ Tính SABC, biết: AB+AC=20cm, BC=12cm.
b/ Gọi D là trung điểm của AB. CD cắt AH tại G. Tính AG, HG (theo đơn vị cm)
cho tam giác ABC có đường cao BE,CF cắt tại H,gọi là trung điểm của AH và K là trung điểm của BC.Biết AH=6cm,BC=8cm.Khi đó độ dài IK là bao nhiêu?
Bài 1: Cho tam giác ABC cân tại A. Vẽ AH vuông góc với BC tại H. Gọi D là trung điểm cạnh AC, G là giao điểm của AH và BD
a) CMR AH là đường trung tuyến của tam giác ABC
b) Gọi N là giao điểm của CG và AB. CMR N là trung điểm của cạnh AB
Cho tam giác ABC cân tại A có góc A=120 độ, kẻ AH vuông góc BC tại H. Gọi D là trung điểm của AB, đường trung trực của AB cắt AB tại D và cắt BC tại E,. Chứng minh:tam giác BED = tam giác AEH
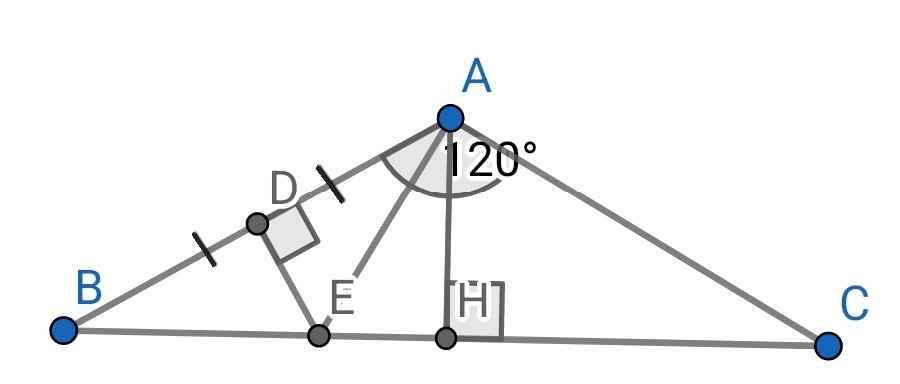Do ∆ABC cân tại A (gt)
⇒ ∠B = ∠C = (180⁰ - ∠BAC) : 2
= (180⁰ - 120⁰) : 2
= 30⁰
∆AHB vuông tại H (do AH ⊥ BC)
⇒ ∠B + ∠BAH = 90⁰
⇒ ∠BAH = 90⁰ - ∠B
= 90⁰ - 30⁰
= 60⁰
Xét hai tam giác vuông: ∆AED và ∆BED có:
ED là cạnh chung
AD = BD (do D là trung điểm của AB)
⇒ ∆AED = ∆BED (hai cạnh góc vuông)
⇒ ∠EAD = ∠EBD = 30⁰ (hai góc tương ứng)
⇒ ∠EAH = ∠BAH - ∠EAD
= 60⁰ - 30⁰
= 30⁰
⇒ ∠EAH = ∠EAD
Xét hai tam giác vuông: ∆AEH và ∆AED có:
AE là cạnh chung
∠EAH = ∠EAD = 30⁰
⇒ ∆AEH = ∆AED (cạnh huyền - góc nhọn)
Mà ∆AED = ∆BED (cmt)
⇒ ∆BED = ∆AEH
Đúng 3
Bình luận (0)
Tam giác ABC cân tại A. Vẽ AH vuông góc BC tại H. Cho AB = AC = 6cm; BC = 4cm .Vẽ trung tuyến BE, CF là trung tuyến. Gọi G là giao điểm của BE, CF
a, C/m H là trung điểm của BC
b, Tính AH
c, C/m tam giác GBC cân
d, AG ?
1) Cho tam giác ABC cân tại A có AH là đường cao
a) Biết AB=8cm, BC=4cm. Tính diện tích tam giác ABC
b) Gọi N là trung điểm của AC. Tứ giác ANHB là hình gì?
2) Cho tam giác ABC cân tại A
a) Biết AB=10cm, BC=5cm. Đường trung tuyến AH. Tính diện tích tam giác ABC
b) Gọi M, N lần lượt là trung điểm của AB,AC. Tứ giác BMNC là hình gì?
Mn giúp mik vs bài này mik cần gấp!
Bài 2:
a: H là trung điểm của BC
nên HB=HC=2,5(cm)
\(\Leftrightarrow AH=\dfrac{5\sqrt{15}}{2}\left(cm\right)\)
\(S=\dfrac{\dfrac{5\sqrt{15}}{2}\cdot5}{2}=\dfrac{25\sqrt{15}}{4}\left(cm^2\right)\)
b: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BMNC là hình thang cân
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A và AH vuông với BC tại H(H thuộc BC)a)Chứng minh tam giác ABHtam giác ACH và H la trung điểm cảu BC.b)Gọi M là trung điểm của AC,BM cắt AH tại I.Qua C kẻ đường thẳng song song với AB,đường thẳng này cắt tia BM tại EChứng minh tam giác AMBtam giác CME và I là trọng tâm của tam giác ABCc)Từ C kẻ đường thẳng vuông góc với CB cắt ME tại K. Chứng minh AB+BC3IK.
Đọc tiếp
Cho tam giác ABC cân tại A và AH vuông với BC tại H(H thuộc BC)
a)Chứng minh tam giác ABH=tam giác ACH và H la trung điểm cảu BC.
b)Gọi M là trung điểm của AC,BM cắt AH tại I.
Qua C kẻ đường thẳng song song với AB,đường thẳng này cắt tia BM tại E
Chứng minh tam giác AMB=tam giác CME và I là trọng tâm của tam giác ABC
c)Từ C kẻ đường thẳng vuông góc với CB cắt ME tại K. Chứng minh AB+BC>3IK.
a) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(cạnh huyền-cạnh góc vuông)
Suy ra: BH=CH(hai cạnh tương ứng)
mà B,H,C thẳng hàng(gt)
nên H là trung điểm của BC(Đpcm)
Đúng 0
Bình luận (0)
b) Xét ΔAMB và ΔCME có
\(\widehat{AMB}=\widehat{CME}\)(hai góc đối đỉnh)
MA=MC(M là trung điểm của AC)
\(\widehat{BAM}=\widehat{ECM}\)(hai góc so le trong, AB//CE)
Do đó: ΔAMB=ΔCME(g-c-g)
Xét ΔABC có
BM là đường trung tuyến ứng với cạnh AC(M là trung điểm của AC)
AH là đường trung tuyến ứng với cạnh BC(H là trung điểm của BC)
BM cắt AH tại I(gt)
Do đó: I là trọng tâm của ΔABC(Tính chất ba đường trung tuyến của tam giác)
Đúng 1
Bình luận (0)
Cho tam giác ABC có các đường cao BE,CF cắt nhau tại H. Gọi I là trung điểm của cạnh BC.Biết AH=6cm,BC=8cm.Khi đó độ dài IK là :
