mn giúp mik nhé! mik đag cần gấp.
Cho tam giác ABC. Có đường cao AH bằng 5cm. HB = 2/5 HC. Tính
diện tích tam giác ABC, biết tam giác AHB có diện tích là 6cm2.
cho tam giác abc có đường cao ah = 4cm, hb =1/3 hc. tính diện tích tam giác abc, biết ta giác ahb có diện tích là 6cm2
\(HB+HC=BC\)
=>\(\dfrac{1}{3}HC+HC=BC\)
=>\(BC=\dfrac{4}{3}HC\)
mà \(HB=\dfrac{1}{3}HC\)
nên \(\dfrac{BC}{HB}=\dfrac{4}{3}:\dfrac{1}{3}=4\)
=>BC=4HB
=>\(S_{ABC}=4\cdot S_{AHB}=4\cdot6=24\left(cm^2\right)\)
Các cậu ơi , giúp tớ với ( tớ đang cần gấp )
Câu 16. Cho tam giác ABC có đường cao AH bằng 40mm, HB = \(\dfrac{2}{3}\)HC. Tính diện tích tam giác ABC, biết tam giác AHB có diện tích 16cm2 ?
Cho tam giác ABC có đường cao AH = 40mm, HB = { EQ \F(2,3) } HC. Tính diện tích tam giác ABC, biết tam giác AHB có diện tích là 16cm2?
2/3 nha mn, Giải chi tiết giúp mik.
Cho tam giác ABC vuông tại A có AH là đường cao. Biết HB= 4cm, HC= 9cm.
a) Tính độ dài đườn cao AH
b) Tính diện tích tam giác ABC
tự vẽ hình
ta có <HBA+<BAH= 90\(^0\)(vì tam giác ABH vg tại H)
Có <BAH+ <HAC= 90\(^0\)(vì tam giác ABC vg tại A)
=> <HBA=<HAC
Xét tam giác BAH và ACH
<BHA=<AHC\(\left(90^0\right)\)
<ABH=<HAC
=> Tam giác BAH đồng dạng với tam giác ACH
=> BH/AH=AH/CH=> AH^2= BH*CH=4*9=36 cm
b, ta có BC=BH+CH=4+9=13 cm
S(ABC) = AH*BC=36*13=468 cm\(^2\)
cho tam giác abc (Â=90độ).
có độ cao AH biết HB=4CM HC=9CM
A)tính ab,ah,ac
B) tính diện tích tam giác abc
Giúp mik vs ạ mik mong rằng sẽ có bn nào giúp
Xét \(\Delta ABC\) và \(\Delta HBA\) có:
\(\widehat{BAC}=\widehat{BHA}=90^o\)
\(\widehat{B}\) chung
\(\Rightarrow\Delta ABC\sim\Delta HBA\left(g.g\right)\) (1)
\(\Rightarrow\dfrac{AB}{BC}=\dfrac{HB}{AB}\) hay \(\dfrac{AB}{4+9}=\dfrac{4}{AB}\Rightarrow AB^2=52\Rightarrow AB=\sqrt{52}=2\sqrt{13}cm\)
Xét \(\Delta\text{A}BC\) và \(\Delta HAC\) có:
\(\widehat{BAC}=\widehat{AHC}=90^o\)
\(\widehat{C}\) chung
\(\Rightarrow\Delta ABC\sim\Delta HAC\left(g.g\right)\) (2)
Từ (1) và (2) \(\Rightarrow\Delta HAB\sim\Delta HCA\)
\(\Rightarrow\dfrac{AH}{HC}=\dfrac{HB}{AH}\) hay \(\dfrac{AH}{9}=\dfrac{4}{AH}\Rightarrow AH^2=36\Rightarrow AH=\sqrt{36}=6\left(cm\right)\)
Ta có \(\Delta ABC\) vuông tại A.
Áp dụng đinh lý Py-ta-go ta có:
\(AC=\sqrt{BC^2-AB^2}=\sqrt{\left(4+9\right)^2-\left(2\sqrt{13}\right)^2}=3\sqrt{13}cm\)
b) Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot BC\cdot AH=\dfrac{1}{2}\cdot\left(4+9\right)\cdot6=39\left(cm^2\right)\)
Cho tam giác ABC có đường cao AH = 4cm, HB = 1/3 HC. Tính diện tích tam giác ABC biết tam giác AHB có diện tích 6cm2
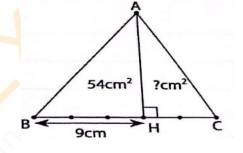
Cho tam giác ABC, đường cao AH (hình vẽ), biết BH = 9cm và HB = 3/2 HC. Tính diện tích tam giác AHC, biết diện tích tam giác AHB là 54cm2 . (tính theo 2 cách). Gợi ý: Cách 1: Áp dụng công thức Cách 2: Tính theo tỉ số tam giác.
Cho tam giác ABC vuông tại A có AH là đường cao.Biết HB=4cm,HC=9cm
a)Tính độ dài AH
b)Tính diện tích tam giác ABC
a)Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow AH^2=4\cdot9=36\)
hay AH=6(cm)
Vậy: AH=6cm
b) Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{AH\cdot BC}{2}=\dfrac{6\cdot13}{2}=39\left(cm^2\right)\)
Cho tam giác ABC góc A=90°AC=4cm Bc=5cm đường cao AH phân giác AD a, tính ac b, chứng minh tam giác ABC đồng giác với tam giác HAC c, AC²=HC.BC ; HB?HC? d, tính DC e, diện tích ABC , diện tích ABC Em cần gấp lắm ạ
a.Áp dụng định lý pitago:
\(AB=\sqrt{5^2-4^2}=\sqrt{9}=3\left(cm\right)\)
b.Xét tam giác ABC và tam giác HAC, có:
\(\widehat{BAC}=\widehat{AHC}=90^o\)
\(\widehat{C}\): chung
Vậy tam giác ABC đồng dạng tam giác HAC ( g.g )
\(\Rightarrow\dfrac{AC}{HC}=\dfrac{BC}{AC}\)
\(\Leftrightarrow AC^2=BC.HC\) ( đfcm )
c.\(\Rightarrow HC=\dfrac{AC^2}{BC}=\dfrac{4^2}{5}=3,2\left(cm\right)\)
\(HB=BC-HC=5-3,2=1,8\left(cm\right)\)
d.Áp dụng t/c đường phân giác \(\widehat{BAC}\) có:
\(\dfrac{AB}{AC}=\dfrac{DB}{DC}\)
\(\Leftrightarrow\dfrac{3}{4}=\dfrac{DB}{DC}\)
\(\Leftrightarrow\dfrac{DC}{4}=\dfrac{DB}{3}=\dfrac{DC+DB}{4+3}=\dfrac{5}{7}\)
\(\Rightarrow DC=\dfrac{5}{7}.4=\dfrac{20}{7}\left(cm\right)\)
e.\(S_{ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.3.4=6\left(cm^2\right)\)