Phân tích đa thức thành nhân tử: a)x3+y3-3xy+1 b) (4-x)5+(x-2)5-32

Những câu hỏi liên quan
Phân tích các đa thức sau thành nhân tử:a) 4
x
2
- 4x + 1; b) 16
y
3
- 2
x
3
- 6x(x + 1) - 2;c) 2
x
2
+7x + 5; d)
x
2
- 6xy - 25
z
2
+9
y
2
Đọc tiếp
Phân tích các đa thức sau thành nhân tử:
a) 4 x 2 - 4x + 1; b) 16 y 3 - 2 x 3 - 6x(x + 1) - 2;
c) 2 x 2 +7x + 5; d) x 2 - 6xy - 25 z 2 +9 y 2
Phân tích các đa thức sau thành nhân tử:a) 2xy + 3z + 6y + xz; b)
a
4
-
9
a
3
+
a
2
- 9a;c) 3
x
2
+ 5y - 3xy + (-5x); d)
x
2
- (a + b)x + ab;e) 4
x
2
- 4xy + ...
Đọc tiếp
Phân tích các đa thức sau thành nhân tử:
a) 2xy + 3z + 6y + xz; b) a 4 - 9 a 3 + a 2 - 9a;
c) 3 x 2 + 5y - 3xy + (-5x); d) x 2 - (a + b)x + ab;
e) 4 x 2 - 4xy + y 2 - 9 t 2 ; g) x 3 – 3 x 2 y + 3x y 2 – y 3 – z 3
h) x2 - y2 + 8x + 6y + 7.
a) Cách 1.
Ta có 2xy + 3z + 6y + xz = (2xy + xz) + (3z + 6y)
= x(2 y + z)+3(z + 2 y) = (z + 2y)(x + 3).
Cách 2.
Ta có 2xy + 3z + 6y + xz = (2x1/ + 6y) + (3z + xz)
= 2y(x + 3) + z(3 + x) = (z + 2y)(x + 3).
b) Biến đổi được a 4 - 9 rt 3 + a 2 -9a = (a- 9)a( a 2 +1).
c) Biến đổi được 3 x 2 + 5y - 3xy + (-5x) = (x - y)(3x - 5).
d) Biến đổi được x 2 - (a + b)x + ab = (x- a)(x - b).
e) Ta có 4 x 2 - 4xy + y 2 – 9 t 2 = ( 2 x - y ) 2 - ( 3 t ) 2
= (2x - y - 3t )(2x - y + 31).
g) Ta có x 3 - 3 x 2 y + 3 xy 2 - y 3 - z 3
= ( x - y ) 3 - z 3 = (x - y - z)( x 2 + y 2 + z 2 - 2xy + xz - yz).
h) Ta có x 2 - y 2 + 8x + 6y+ 7 = ( x 2 +8x + 16) - ( y 2 - 6y+ 9)
= ( x + 4 ) 2 - ( y - 3 ) 2 =(x-y + 7)(x + y + l).
Đúng 0
Bình luận (0)
x3– x + 3x2y + 3xy2 + y3– y=? (Phân tích đa thức thành nhân tử)
\(=\left(x+y\right)^3-\left(x+y\right)=\left(x+y\right)\left(x^2+2xy+y^2-1\right)\)
Đúng 1
Bình luận (0)
\(x^3-x+3x^2+3xy^2+y^3-y\)
\(=\left(x+y\right)^3-\left(x+y\right)\)
\(=\left(x+y\right)\left(x+y+1\right)\left(x+y-1\right)\)
Đúng 1
Bình luận (0)
= (x3 + 3x2y + 3xy2 + y3) - (x+y)
= (x + y)3 - (x + y)
= (x + y).[(x+y)2 - 1 ]
= (x + y).(x + y - 1).(x + y + 1)
Đúng 1
Bình luận (3)
Phân tích đa thức thành nhân tử:a)
(
3
x
+
l
)
2
-
(
3
x
-
l
)
2
; b)
(
x
...
Đọc tiếp
Phân tích đa thức thành nhân tử:
a) ( 3 x + l ) 2 - ( 3 x - l ) 2 ; b) ( x + y ) 2 - ( x - y ) 2 ;
c) ( x + y ) 3 - ( x - y ) 3 ; d) x 3 + y 3 + z 3 - 3xyz.
a) 12x. b) 4xy
c) 2y(3 x 2 + y 2 ).
d) (x + y + z)( x 2 + y 2 + z 2 – xy – xz - yz).
Đúng 0
Bình luận (0)
Phan tích đa thức thành nhân tử
1. (b-c)3+(c-a)3+(a-b)3
2. x3+y3+z3-3xyz
3. (x+y)5-x5-y5
4. (x2+y2)3+(z2-x2)3-(y2+z2)3
5. x3-5x2y-14xy2
1. Ta có: hằng đẳng thức: \(x^3+y^3+z^3=3xyz\) nếu x+y+z=0
đặt b-c=x, c-a=y, a-b=z⇒x+y+z=0
\(\Rightarrow\left(b-c\right)^3+\left(c-a\right)^3+\left(a-b\right)^3=3\left(a-b\right)\left(c-a\right)\left(b-c\right)\)
2. \(x^3+y^3+z^3-3xyz=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-zx\right)+3xyz-3xyz=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-zx\right)\)
3. Tham khảo: https://hoc247.net/hoi-dap/toan-8/phan-tich-da-thuc-x-y-5-x-5-y-5-thanh-nhan-tu-faq447273.html
Đúng 1
Bình luận (0)
\(5,=x^3+2x^2y-7x^2y-14xy^2\\ =x^2\left(x+2y\right)-7xy\left(x+2y\right)\\ =x\left(x-7y\right)\left(x+2y\right)\)
Đúng 2
Bình luận (0)
phân tích đa thức thành nhân tử
( x + y - z)3 - x3 - y3 + z3
\(\left(x+y-z\right)^3-x^3-y^3+z^3\)
\(=\left[\left(x+y\right)-z\right]^3-x^3-y^3+z^3\)
\(=\left(x+y\right)^3-z^3-3\left(x+y\right)z\left(x+y-z\right)-x^3-y^3+z^3\)
\(=x^3+y^3-z^3+3xy\left(x+y\right)-3\left(x+y\right)z\left(x+y-z\right)-x^3-y^3+z^3\)
\(=3xy\left(x+y\right)-3z\left(x+y\right)\left(x+y-z\right)\)
\(=3\left(x+y\right)\left[xy-z\left(x+y-z\right)\right]\)
\(=3\left(x+y\right)\left(xy-zx-yz+z^2\right)\)
\(=3\left(x+y\right)\left[x\left(y-z\right)-z\left(y-z\right)\right]\)
\(=3\left(x+y\right)\left(y-z\right)\left(x-z\right)\)
#\(Urushi\text{☕}\)
Đúng 2
Bình luận (0)
Áp dụng (a+b)3 = a3+b3+3ab(a+b), ta có:
(x+y+z)3-x3-y3-z3
=[(x+y)+z]3-x3-y3-z3
=(x+y)3+z3+3z(x+y)(x+y+z)-x3-y3-z3
=x3+y3+3xy(x+y)+z3+3z(x+y)(x+y+z)-x3-y3-z3
=3(x+y)(xy+xz+yz+z2)
=3(x+y)[x(y+z)+z(y+z)]
=3(x+y)(y+z)(x+z)
Đúng 0
Bình luận (2)
=(x+y-z-x)[(x+y-z)^2+x(x+y-z)+x^2]-(y-z)(y^2+yz+z^2)
=(y-z)(x^2+y^2+z^2+2xy-2xz-2yz+x^2+xy-xz+x^2-y^2-yz-z^2)
=(y-z)(3x^2+3xy-3xz-3yz)
=3(y-z)(x^2+xy-xz-yz)
=3(y-z)[x(x+y)-z(x+y)]
=3(y-z)(x+y)(x-z)
Đúng 0
Bình luận (0)
Phân tích các đa thức sau thành nhân tử:a)
(
4
t
+
2
)
3
+
8
(
1
-
2
t
)
3
; b)
x
3...
Đọc tiếp
Phân tích các đa thức sau thành nhân tử:
a) ( 4 t + 2 ) 3 + 8 ( 1 - 2 t ) 3 ; b) x 3 + y 3 - z 3 +3xyz.
a) 16(12 t 2 +1).
b) Gợi ý x 3 + y 3 = ( x + y ) 3 - 3xy(x + y)
(x + y - z)( x 2 + y 2 + z 2 - xy + xz + yz).
Đúng 0
Bình luận (0)
Phân tích các đa thức sau thành nhân tử:1) x3 - 7x + 62) x3 - 9x2 + 6x + 163) x3 - 6x2 - x + 304) 2x3 - x2 + 5x + 35) 27x3 - 27x2 + 18x - 46) x2 + 2xy + y2 - x - y - 127) (x + 2)(x +3)(x + 4)(x + 5) - 248) 4x4 - 32x2 + 19) 3(x4 + x2 + 1) - (x2 + x + 1)210) 64x4 + y411) a6 + a4 + a2b2 + b4 - b612) x3 + 3xy + y3 - 113) 4x4 + 4x3 + 5x2 + 2x + 114) x8 + x + 115) x8 + 3x4 + 416) 3x2 + 22xy + 11x + 37y + 7y2 +1017) x4 - 8x + 63
Đọc tiếp
Phân tích các đa thức sau thành nhân tử:
1) x3 - 7x + 6
2) x3 - 9x2 + 6x + 16
3) x3 - 6x2 - x + 30
4) 2x3 - x2 + 5x + 3
5) 27x3 - 27x2 + 18x - 4
6) x2 + 2xy + y2 - x - y - 12
7) (x + 2)(x +3)(x + 4)(x + 5) - 24
8) 4x4 - 32x2 + 1
9) 3(x4 + x2 + 1) - (x2 + x + 1)2
10) 64x4 + y4
11) a6 + a4 + a2b2 + b4 - b6
12) x3 + 3xy + y3 - 1
13) 4x4 + 4x3 + 5x2 + 2x + 1
14) x8 + x + 1
15) x8 + 3x4 + 4
16) 3x2 + 22xy + 11x + 37y + 7y2 +10
17) x4 - 8x + 63
1) \(x^2-7x+6=x^3+1-7x-7=\left(x^3+1\right)-7\left(x+1\right)=\left(x+1\right)\left(x^2-x-6\right)\)
2) \(x^3-9x^2+6x+16\)
\(\left(x^3+1\right)-\left[\left(9x^2-6x+1\right)-16\right]\)
\(=\left(x^3+1\right)-\left[\left(3x-1\right)^2-16\right]=\left(x^3+1\right)-\left(3x-1+4\right)\left(3x-1-4\right)\)\(=\left(x^3+1\right)-3\left(3x-5\right)\left(x+1\right)\)\(=\left(x+1\right)\left[x^2-x+1-9x+15\right]=\left(x+1\right)\left(x^2-10x+16\right)\)
\(=\left(x+1\right)\left[x\left(x-2\right)-8\left(x-2\right)\right]\)\(\left(x+1\right)\left(x-2\right)\left(x-8\right)\)
3) \(x^3-6x^2-x+30\)
\(=x^3-5x^2-x^2+5x-6x+30\)
\(=x^2\left(x-5\right)-x\left(x-5\right)-6\left(x-5\right)\)
\(=\left(x-5\right)\left(x^2-x-1\right)\)
4) \(2x^3-x^2+5x+3=\left(2x^3+x^2\right)-\left(2x^2+x\right)+\left(6x+3\right)\)
\(=x^2\left(2x+1\right)-x\left(2x+1\right)+3\left(2x+1\right)\)
\(=\left(2x+1\right)\left(x^2-x+3\right)\)
5) \(27x^3-27x^2+18x-4=\left(27x^3-1\right)-\left(27x^2-18x+3\right)\)
\(=\left(3x-1\right)\left(9x^2+3x+1\right)-3\left(9x^2-6x+1\right)\)
\(=\left(3x-1\right)\left(9x^2+3x+1\right)-3\left(3x-1\right)^2\)
\(=\left(3x-1\right)\left(9x^2+3x+1-9x+3\right)=\left(3x-1\right)\left(9x^2-6x+4\right)\)
gửi phần này trước còn lại làm sau !!! tk mk nka !!!
Đúng 0
Bình luận (0)
6) \(\left(x+y\right)^2-\left(x+y\right)-12\)\(=\left(x+y\right)^2-2\cdot\frac{1}{2}\left(x+y\right)+\frac{1}{4}-\frac{49}{4}\)
\(=\left(x+y-\frac{1}{2}\right)^2-\left(\frac{7}{2}\right)^2\)\(=\left(x+y-\frac{1}{2}-\frac{7}{2}\right)\left(x+y-\frac{1}{2}+\frac{7}{2}\right)\)
\(=\left(x-4\right)\left(x+3\right)\)
7) \(\left(x+2\right)\left(x+5\right)\left(x+3\right)\left(x+4\right)-24\) (NHÂN x + 2 vs x + 5 và x + 3 vs x + 4 )
\(=\left(x^2+7x+10\right)\left(x^2+7x+12\right)-24\)
ĐẶT \(x^2+7x+11=y\) ta được :
\(\left(y+1\right)\left(y-1\right)-24=y^2-1-24\)
\(=y^2-25=\left(y-5\right)\left(y+5\right)\)
8) \(4x^4-32x^2+1=4x^4+4x^2+1-36x^2\)
\(=\left(2x^2+1\right)^2-\left(6x\right)^2\)\(=\left(2x^2-6x+1\right)\left(2x^2+6x+1\right)\)
9) sai đề rùi bạn ơi ! đề đúng nè
\(3\left(x^4+x^2+1\right)-\left(x^2+x+1\right)^2\)
Ta thấy :
\(x^4+x^2+1=\left(x^4+2x^2+1\right)-x^2\)\(=\left(x^2+1\right)^2-x^2=\left(x^2+x+1\right)\left(x^2-x+1\right)\)
Thay vào biểu thức bài cho ta được :
\(3\left(x^2-x+1\right)\left(x^2+x+1\right)-\left(x^2+x+1\right)^2\)
\(=\left(x^2+x+1\right)\left(3x^2-3x+3-x^2-x-1\right)\)
\(=\left(x^2+x+1\right)\left(2x^2-4x+2\right)\)
\(=2\left(x^2+x+1\right)\left(x-1\right)^2\)
bài ở trên câu 3 : kết luận là \(\left(x-3\right)\left(x^2-x-6\right)\)bạn sửa lại giúp mk nka !!! Th@nk !!! Tk Mk vs
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Phân tích đa thức thành nhân tử:(x-y)z3 + (y-z)x3+ (z-x)y3
Ta có: ( x - y) z3 + ( y - z ) x3 + ( z - x ) y3
= ( x - y ) z3 + ( y - z )x3 + ( z - y)y3 + ( y - x ) y3
= ( x - y ) ( z3 - y3 ) + ( y - z ) ( x3 - y3)
= ( x - y ) ( z - y ) ( z2 + zy + y2 ) + ( y - z ) ( x - y) ( x2 + xy + y2 )
= ( x - y ) ( y - z ) ( x2 + xy + y2 - z2 - zy - y2)
= ( x - y ) ( y - z ) [ ( x2 - z2) + ( xy - zy) ]
= ( x - y ) ( y - z ) [ ( x - z ) ( x + z ) + y ( x - z ) ]
= ( x - y ) ( y - z ) ( x - z ) ( x + y + z )




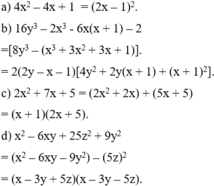

 k cho tui nha
k cho tui nha


















