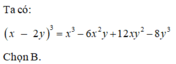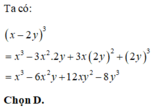5/6x2y + 7/12xy2

Những câu hỏi liên quan
x3-6x2y+12xy2-1
\(Sửa:x^3-6x^2y+12xy^2-8y^3=\left(x-2y\right)^3\)
Đúng 0
Bình luận (0)
Kết quả phân tích đa thức 6 x 2 y – 12 x y 2 là:
A. 6xy(x – 2y)
B. 6xy(x – y)
C. 6xy(x + 2y)
D. 6xy(x + y)
6 x 2 y – 12 x y 2 = 6xy.x – 6xy.2y = 6xy(x – 2y)
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Phân tích đa thức
x
3
–
6
x
2
y
+
12
x
y
2
–
8
y
3
thành nhân tử A.
(
x
–
y...
Đọc tiếp
Phân tích đa thức x 3 – 6 x 2 y + 12 x y 2 – 8 y 3 thành nhân tử
A. ( x – y ) 3
B. ( 2 x – y ) 3
C. x 3 – ( 2 y ) 3
D. ( x – 2 y ) 3
x 3 – 6 x 2 y + 12 x y 2 – 8 y 3 = x 3 – 3 . x 2 . ( 2 y ) + 3 . x . ( 2 y ) 2 – ( 2 y ) 3 = ( x – 2 y ) 3
đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Khai triển biểu thức
x
–
2
y
3
ta được kết quả làA.
x
3
–
8
y
3
B.
x
3
–
2
y
3
C.
x
3...
Đọc tiếp
Khai triển biểu thức x – 2 y 3 ta được kết quả là
A. x 3 – 8 y 3
B. x 3 – 2 y 3
C. x 3 – 6 x 2 y + 6 x y 2 – 2 y 3
D. x 3 – 6 x 2 y + 12 x y 2 – 8 y 3
Khai triển biểu thức
(
x
-
2
y
)
3
ta được kết quả là:A.
x
3
-
8
y
3
B.
x
3
-
2
y
3
C.
x
3
−
6
x...
Đọc tiếp
Khai triển biểu thức ( x - 2 y ) 3 ta được kết quả là:
A. x 3 - 8 y 3
B. x 3 - 2 y 3
C. x 3 − 6 x 2 y + 6 x y 2 − 2 y 3
D. x 3 − 6 x 2 y + 12 x y 2 − 8 y 3
Viết biểu thức x 3 - 6 x 2 y + 12 x y 2 - 8 y 3 dưới dạng lập phương của một hiệu
Ta có : x 3 - 6 x 2 y + 12 x y 2 - 8 y 3 = ( x ) 3 - 3 . x 2 . 2 y + 3 . x . ( 2 y ) 2 - ( 2 y ) 3 = ( x - 2 y ) 3
Đúng 0
Bình luận (0)
Viết biểu thức x 3 - 6 x 2 y + 12 x y 2 - 8 y 3 dưới dạng lập phương của một hiệu.
Ta có : x 3 - 6 x 2 y + 12 x y 2 - 8 y 3 = ( x ) 3 - 3 . x 2 . 2 y + 3 . x . ( 2 y ) 2 - ( 2 y ) 3 = ( x - 2 y ) 3
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức:
x3 - 6x2y + 12xy2 - 8y3
l) 5xy2- 10xyz + 5xz2
m) x3+ 3x2+ 3x + 1 - 27y3
n) x2- 6xy + 9y2
o) x3+ 6x2y + 12xy2+ 8y3
p) 125x3+ y6
q) x2 + 4xy + 4y2 - 2x - 4y + 1
\(l,=5x\left(y^2-2yz+5z\right)\\ m,=\left(x+1\right)^3-27y^3\\ =\left(x+1-3y\right)\left(x^2+2x+1+3xy+3y+9y^2\right)\\ n,=\left(x-3y\right)^2\\ o,=\left(x+2y\right)^3\\ p,=\left(5x+y^2\right)\left(25x^2-5xy^2+y^4\right)\\ q,=\left(x+2y\right)^2-2\left(x-2y\right)+1\\ =\left(x+2y-1\right)^2\)
Đúng 0
Bình luận (0)