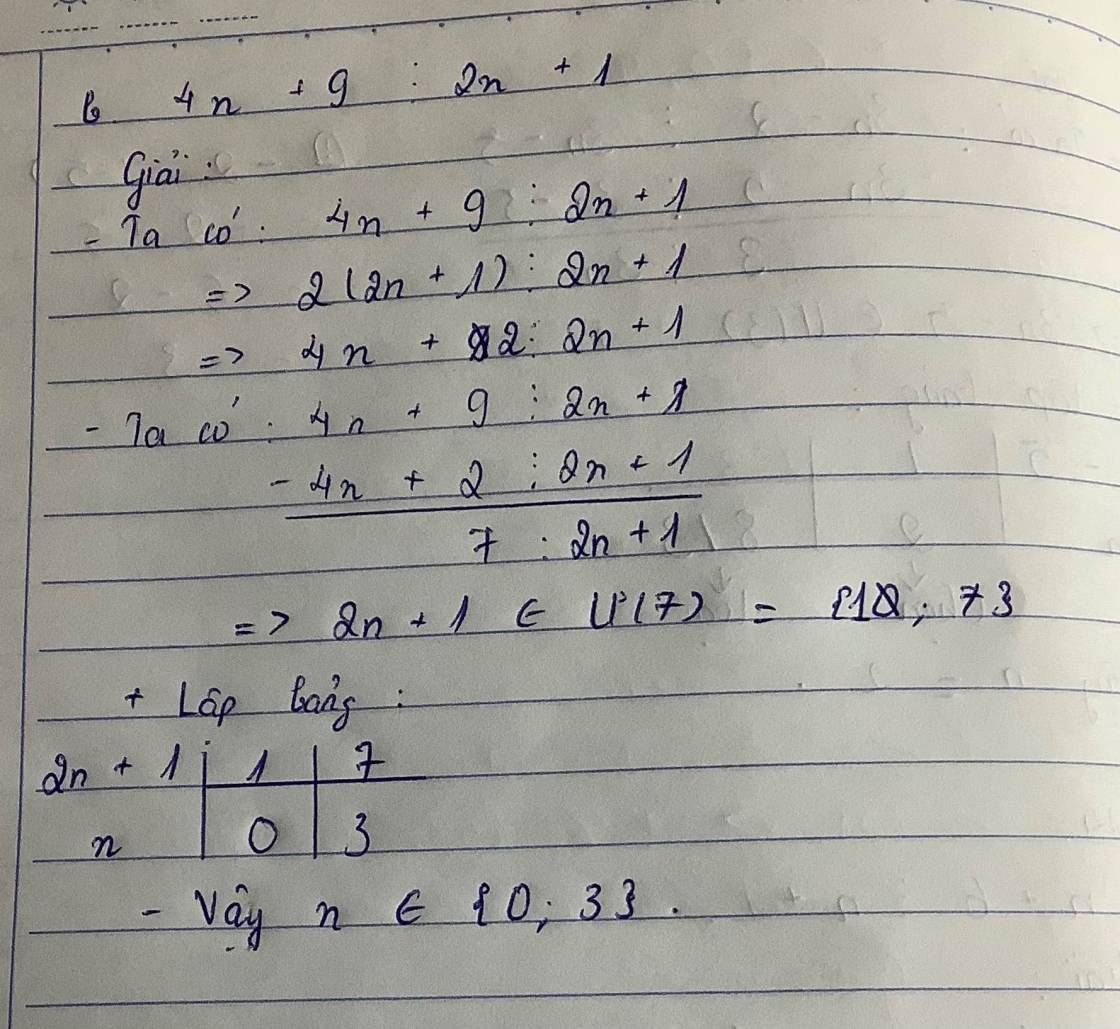TÌM SỐ NGUYÊN N SAO CHO 4N - 9 CHIA HẾT CHO 2N + 1

Những câu hỏi liên quan
tìm số nguyên n sao cho 4n-9 chia hết cho 2n+1
tìm số nguyên n sao cho 4n-9 chia hết cho 2n+1
4n-9 = 4n+2-11 = 2(2n+1)-11. Nhận thấy: 2(2n+1) chia hết cho 2n+1 với mọi n
=> Để (4n-9) chia hết cho 2n+1 thì 11 phải chia hết cho 2n+1
=> 2n+1 = (-11,-1,1,11)
| 2n+1 | -11 | -1 | 1 | 11 |
| n | -6 | -1 | 0 | 5 |
Đúng 0
Bình luận (0)
Tìm số nguyên n sao cho 4n-9 chia hết cho 2n+1
tìm số nguyên n sao cho 4n+9 chia hết cho 2n+1
\(4n+9=4n+2+7=2\left(2n+1\right)+7\)chia hết cho \(2n+1\)
tương đương với \(7\div\left(2n+1\right)\)mà \(n\)nguyên nên
\(2n+1\inƯ\left(7\right)=\left\{-7,-1,1,7\right\}\)
\(\Leftrightarrow n\in\left\{-4,-1,0,3\right\}\).
tìm số nguyên n sao cho 4n + 9 chia hết cho 2n + 3
tìm số nguyên n sao cho: 4n+3 chia hết cho 2n+1
`4n+3 vdots 2n+1`
`=>4n+2+1 vdots 2n+1`
`=>2(2n+1)+1 vdots 2n+1`
`=>1 vdots 2n+1`
`=>2n+1 in Ư(1)={1,-1}`
`*2n+1=1=>2n=0=>n=0(tm)`
`*2n+1=-1=>2n=-2=>n=-1(tm)`
Vậy `n in {0;-1}` thì `4n+3 vdots 2n+1`
Đúng 2
Bình luận (0)
\(4n+3⋮2n+1\Leftrightarrow2\left(2n+1\right)+1⋮2n+1\Leftrightarrow1⋮2n+1\)
\(\Rightarrow2n+1\inƯ\left(1\right)=\left\{\pm1\right\}\)
| 2n + 1 | 1 | -1 |
| n | 0 | -1 |
Đúng 2
Bình luận (0)
4n + 3 chia hết cho 2n + 1 ( 1 )
Mà 2( 2n + 1 ) chia hết cho 2n + 1 ⇒ 4n + 2 \(⋮\) 2n + 1 ( 2 )
Từ (1) và (2) suy ra: ( 4n + 3 ) - ( 4n + 2 ) chia hết cho 2n + 1 \(\Rightarrow\) 1 \(⋮\) 2n + 1
⇒ 2n + 1 ∈ \(Ư_{\left(1\right)}=\left\{1\right\}\)
2n + 1 =1
2n = 0
⇒ n = 0
Đúng 0
Bình luận (1)
Tìm số nguyên n sao cho :
a ) 4n - 5 : 2n -1
b) 2- 4n chia hết cho n-1
c) n^2 + 3n + 1 : n + 1
D) 3 n + 5 chia hết cho n -2
a: \(\Leftrightarrow2n-1\in\left\{1;-1;3;-3\right\}\)
hay \(n\in\left\{1;0;2;-1\right\}\)
c: \(\Leftrightarrow n+1\in\left\{1;-1\right\}\)
hay \(n\in\left\{0;-2\right\}\)
Đúng 2
Bình luận (0)
Tìm số nguyên n sao cho
a, (4n-5)chia het cho (2n+1)
b,(n+7) chia hết cho n^2+2
c, 4n^2-1 chia hét cho (2n-1)
Tìm số nguyên n sao cho 4n-5 chia hết cho 2n-1
nếu 4n-5 chia het cho2n-1 thì :
4n -5=2(2n -1) -4 chia hết cho 2n -1
=>4chia hết cho 2n-1
=>2n-1 thuộc 1,2,4
=> n thuộc 1,3/2,5/2
Đúng 0
Bình luận (0)