Cho tam giác ABC và tam giác A’B’C’ có AC = A’C’, BC = B’C’. Tìm thêm điều kiện để ABC =A’B’C
Cho tam giác ABC và tam giác A’B’C’ có góc A= góc A’=90 độ và BC/B’C’=AC/A’C’.C/m tam giác ABC~tam giác A’B’C’
Cho 2 tam giác ABC và A’B’C’ có kích thước:
Tam giác ABC: AB=6; BC=12;AC=9
Tam giác A’B’C’: A’B’=4,A’C’=6, B’C’=8
Vẽ thêm tam giác A’B’C’ có :
A’B’ = 2cm ; ∠B' = 70o; B’C’ = 3cm
Hãy đo để kiểm nghiệm rằng AC = A’C’. Ta có thể kết luận được tam giác ABC bằng tam giác A’B’C’ hay không ?
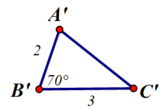
Ta có thể kết luận được tam giác ABC bằng tam giác A’B’C’ (trường hợp c.g.c)
Cho hai tam giác ABC và A’B’C’ có góc ABC + góc A’B’C’ = 180 độ
AB = A’B’ , AC= A’C’
Gọi M là trung điểm của cạnh BC . cMR AM = 1 phần 2 B’C’
Cho hai tam giác ABC và A’B’C’ (Hình 47) có: AB = A’B’ = 2 cm, \(\widehat A = \widehat {A'} = 60^\circ \), AC = A’C’ = 3 cm. Bằng cách đếm số ô vuông, hãy so sánh BC và B’C’. Từ đó có thể kết luận được hai tam giác ABC và A’B’C’ bằng nhau hay không?
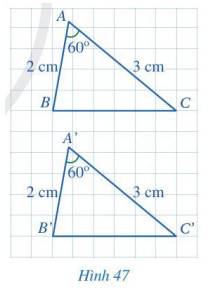
BC = B’C’ = 6 (ô vuông).
Tam giác ABC và A’B’C’ có các cặp cạnh tương ứng bằng nhau nên tam giác ABC bằng tam giác A’B’C’ (c.c.c)
Vẽ thêm tam giác A’B’C’ có :
A’B’ = 2 cm ; B’C’ = 4cm ; A’C’ = 3 cm
Hãy đo rồi so sánh các góc tương ứng của tam giác ABC ở mục 1 và tam giác A’B’C’. Có nhận xét gì về hai tam giác trên ?
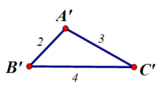
Hai tam giác trên có :
∠A = ∠A' ; ∠B = ∠B' ; ∠C = ∠C'
Nhận xét: Hai tam giác trên bằng nhau
Cho tam giác ABC và tam giác A’B’C’ có góc A + góc A’ = 180 độ và AB = A’B’ , AC = A’C’. M là trung điểm BC. Chứng minh AM = 1/2 B’C’
Cho hai tam giác ABC và A’B’C’ (hình 60)
Hãy dùng thước chia khoảng và thước đo góc để kiểm nghiệm rằng trên hình đó ta có:
AB = A’B’; AC = A’C’ ; BC = B’C’ ; ∠A = ∠A' ; ∠B = ∠B' ; ∠C = ∠C'
Giá để đồ ở Hình 33 gợi nên hình ảnh hai tam giác ABC và A’B’C’ có: AB = A’B’, BC = B’C’, CA = C’A’.
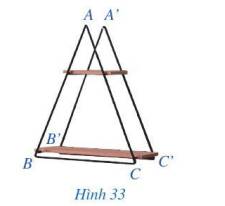
Tam giác ABC có bằng tam giác A’B’C’ hay không?
Tam giác ABC có bằng tam giác A’B’C’ (vì 2 tam giác này có thể chồng khít lên nhau).