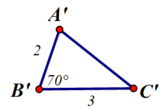
Ta có thể kết luận được tam giác ABC bằng tam giác A’B’C’ (trường hợp c.g.c)
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Vẽ thêm tam giác A’B’C’ có : B’C’ = 4cm ; ∠B' = 60o; ∠C' = 40o. Hãy đo để kiểm nghiệm rằng AB = A’B’. Vì sao ta kết luận được ΔABC = ΔA’B’C’?
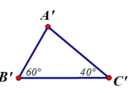
Cho hai tam giác ABC và A’B’C’ (hình 60)
Hãy dùng thước chia khoảng và thước đo góc để kiểm nghiệm rằng trên hình đó ta có:
AB = A’B’; AC = A’C’ ; BC = B’C’ ; ∠A = ∠A' ; ∠B = ∠B' ; ∠C = ∠C'
Vẽ thêm tam giác A’B’C’ có :
A’B’ = 2 cm ; B’C’ = 4cm ; A’C’ = 3 cm
Hãy đo rồi so sánh các góc tương ứng của tam giác ABC ở mục 1 và tam giác A’B’C’. Có nhận xét gì về hai tam giác trên ?
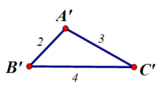
Cho hai tam giác ABC và A’B’C’ có góc ABC + góc A’B’C’ = 180 độ
AB = A’B’ , AC= A’C’
Gọi M là trung điểm của cạnh BC . cMR AM = 1 phần 2 B’C’
Cho tam giác ABC và tam giác A’B’C’ có góc A + góc A’ = 180 độ và AB = A’B’ , AC = A’C’. M là trung điểm BC. Chứng minh AM = 1/2 B’C’
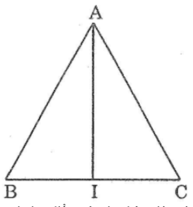
Cắt tam giác ABC bằng giấy có AB = AC và gấp hình theo tia phân giác của góc A. Nếu gấp chia tam giác ABC thành hai tam giác. Hãy đo để kiểm tra xem hai tam giác đó có bằng nhau hay không?
Bài toán ; Vẽ tam giác ABC, biết AB=2cm, BC=4cm, AC=3cm
vẽ thêm Tam giác A'B'C' có:
A'B' = 2cm
B'C' = 4cm
A'C' = 3cm
Hãy đo rồi so sánh các góc tương ứng của tam giác ABC và tam giác A'B'C'. Có nhận xét gì về hai tam giác trên.
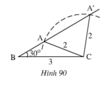
Trên hình 90, các tam giác ABC và ABC có cạnh chung BC 3cm, CA CA’ 2cm,
A
B
C
^
A
B
C
^
30
o
nhưng hai tam giác đó không bằng nhau. Tại sao ở đây không thể áp dụng trường hợp c-g-c để kết luận
Đọc tiếp
Trên hình 90, các tam giác ABC và A'BC có cạnh chung BC = 3cm, CA = CA’ = 2cm, A B C ^ = A ' B C ^ = 30 o nhưng hai tam giác đó không bằng nhau.
Tại sao ở đây không thể áp dụng trường hợp c-g-c để kết luận
Vẽ tam giác ABC có AB = AC = 6cm; BC = 2cm. Sau đó đo góc A để kiểm tra rằng ∠A ≈20o