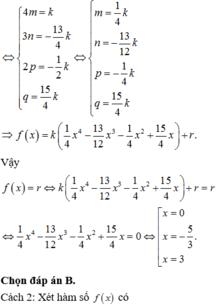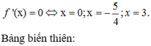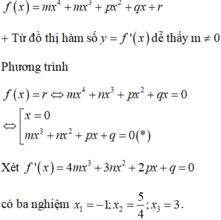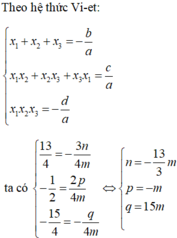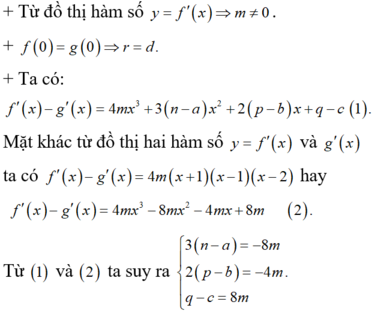Cho phương trình px2 + qx +1 = 0 (1) với p;q là các số hữu tỉ . Biết \(x=\frac{\sqrt{5}-\sqrt{3}}{\sqrt{5}+\sqrt{3}}\) là nghiệm của (1) khi đó p+q = ...

Những câu hỏi liên quan
Cho hàm số
f
(
x
)
m
x
4
+
n
x
3
+
p
x
2
+
q
x
+
r
. Hàm số y f(x) có đồ thị như hình vẽ bên. Tập nghiệm của phương trình f(x) r có số phần tử là A.4. B. 3. C. 1....
Đọc tiếp
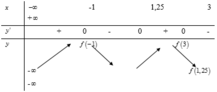
Cho hàm số f ( x ) = m x 4 + n x 3 + p x 2 + q x + r . Hàm số y = f'(x) có đồ thị như hình vẽ bên. Tập nghiệm của phương trình f(x) = r có số phần tử là
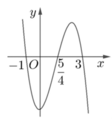
A.4.
B. 3.
C. 1.
D. 2.
Cho hàm số
f
x
m
x
4
+
n
x
3
+
p
x
2
+
q
x
+
r
(
m
,
n
,
p
,
q
,
r
∈
R
)
. Hàm số yf(x) có đồ thị như hình vẽ bên. Tập nghiệm của phương trình f(x)r có số phần tử là A....
Đọc tiếp
Cho hàm số f x = m x 4 + n x 3 + p x 2 + q x + r ( m , n , p , q , r ∈ R ) . Hàm số y=f'(x) có đồ thị như hình vẽ bên. Tập nghiệm của phương trình f(x)=r có số phần tử là
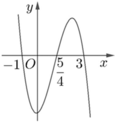
A. 4
B. 3
C. 1
D. 2
Cho hàm số
f
x
m
x
4
+
n
x
3
+
p
x
2
+
q
x
+
r
m
,
n
,
p
,
q
,
r
...
Đọc tiếp
Cho hàm số f x = m x 4 + n x 3 + p x 2 + q x + r m , n , p , q , r ∈ ℝ . Hàm số y = f¢(x) có đồ thị như hình vẽ bên.
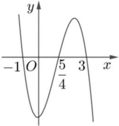
Tập nghiệm của phương trình f (x) = r có số phần tử là
A. 4
B. 3
C. 1
D. 2
Cho hàm số
f
(
x
)
m
x
4
+
n
x
3
+
p
x
2
+
q
x
+
r
(
m
,
n
,
p
,
q
,
r
∈
ℝ
)...
Đọc tiếp
Cho hàm số f ( x ) = m x 4 + n x 3 + p x 2 + q x + r ( m , n , p , q , r ∈ ℝ ) .Hàm số y=f'(x) có đồ thị như hình vẽ bên dưới
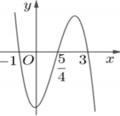
Tập nghiệm của phương trình f(x) = r có số phần tử là
A. 4
B. 2
C. 3
D. 1
Cho các hàm số
f
x
m
x
4
+
n
x
3
+
p
x
2
+
q
x
+
r
và
g
x
a
x
3
+
b
x
2
+
c
x
+
d
thỏa mãn...
Đọc tiếp
Cho các hàm số f x = m x 4 + n x 3 + p x 2 + q x + r và g x = a x 3 + b x 2 + c x + d thỏa mãn f 0 = g 0 . Các hàm số y = f ' x và g ' x có đồ thị như hình vẽ bên. Tập nghiệm của phương trình có số phần tử là
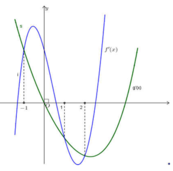
A. 4
B. 2
C. 1
D. 3
Cho hàm số
f
x
m
x
4
+
n
x
3
+
p
x
2
+
q
x
+
r
m
≠
0
. Chia
f
x
cho
x
-
2
được phần dư bằng 2019, chia
f...
Đọc tiếp
Cho hàm số f x = m x 4 + n x 3 + p x 2 + q x + r m ≠ 0 . Chia f x cho x - 2 được phần dư bằng 2019, chia f ' x cho x - 2 được phần dư bằng 2018. Gọi g x là phần dư khi chia f x cho x - 2 2 . Giá trị của g - 1 là
A. - 4033
B. - 4035
C. - 4039
D. - 4037
Do f x chi cho x - 2 được phần dư là 2019 nên ta viết lại:
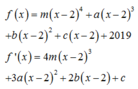
Do f ' x chi cho x - 2 dư 2018 nên c = 2018 .
Suy ra
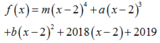
Từ đó phần dư khi chia
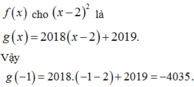
Chọn B.
Đúng 0
Bình luận (0)
Cho phương trình px2+ qx + 1 =0 (1) với p, q là các số hữu tỉ. Biết \(x=\frac{\sqrt{5}-\sqrt{3}}{\sqrt{5}+\sqrt{3}}\) là nghiệm của (1), khi đó p +q =
Cho phương trình bậc hai:
x
2
– qx + 50 0. Tìm q 0 và 2 nghiệm
x
1
;
x
2
của phương trình biết rằng
x
1
2
x
2
A.
q
5
;
x
1
...
Đọc tiếp
Cho phương trình bậc hai: x 2 – qx + 50 = 0. Tìm q > 0 và 2 nghiệm x 1 ; x 2 của phương trình biết rằng x 1 = 2 x 2
A. q = 5 ; x 1 = 10 ; x 2 = 5
B. q = 15 ; x 1 = 10 ; x 2 = 5
C. q = 5 ; x 1 = 5 ; x 2 = 10
D. q = − 15 ; x 1 = − 10 ; x 2 = − 5
biết rằng phương trình \(x^2+px+1=0\) có nghiệm là a,b và phương trình \(x^2+qx+2=0\) có nghiêm là b,c . Khi đó giá trị của biểu thức \(A=pq-\left(b-a\right)\left(b-c\right)\)bằng ?
Áp dụng viet vào pt \(x^2+px+1=0\) ta được:\(\left\{{}\begin{matrix}a+b=-p\\ab=1\end{matrix}\right.\)
Áp dụng viet vào pt \(x^2+qx+2=0\) ta được:\(\left\{{}\begin{matrix}b+c=-q\\bc=2\end{matrix}\right.\)
\(A=pq-\left(b-a\right)\left(b-c\right)=-\left(a+b\right).-\left(b+c\right)-\left(b^2-bc-ab+ac\right)\)
\(=ab+ac+b^2+bc-b^2+bc+ab-ac\)
\(=2ab+2bc=6\)
Đúng 3
Bình luận (0)
Phương trình: \(x^2+px+1=0\)
Có 2 nghiệm:a,b
\(\Rightarrow\left\{{}\begin{matrix}a+b=-p\\a.b=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}p=-\left(a+b\right)\\1=a.b\end{matrix}\right.\)
Phương trình \(x^2+px+2=0\)
Có 2 nghiệm:b,c
\(\Rightarrow\left\{{}\begin{matrix}b+c=-q\\b.c=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}q=-\left(b+c\right)\\2=b.c\end{matrix}\right.\)
Ta có: \(p.q-\left(b-a\right)\left(b-c\right)\)
\(=-\left(a+b\right).\left[-\left(b+c\right)\right]-\left(b-a\right)\left(b-c\right)\)
\(=\left(a+b\right)\left(b+c\right)-\left(b-a\right)\left(b-c\right)\)
\(=ab+ac+b^2+bc-b^2+bc+ab-ac\)
=\(\left(ab+ab\right)+\left(ac-ac\right)+\left(b^2-b^2\right)+\left(bc+bc\right)\)
\(=2ab+2bc\)
\(=2.1+2.2\)
=6
-Chúc bạn học tốt-
Đúng 1
Bình luận (0)