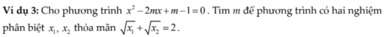
\(\Delta'=m^2-\left(m-1\right)=m^2-m+1=\left(m-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\)

Vậy pt luôn có 2 nghiệm pb 

Ta có : \(x_1+x_2+2\sqrt{x_1x_2}=4\Leftrightarrow2m+2\sqrt{m-1}=4\)

\(\Leftrightarrow\sqrt{m-1}=2-m\)

đk : m =< 2 

TH1 \(m-1=2-m\Leftrightarrow m=\dfrac{3}{2}\)(tm)

TH2 \(m-1=m-2\)( vô lí ) 

\(\Delta'=m^2-m+1=\left(m-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0;\forall m\Rightarrow\) pt luôn có 2 nghiệm pb

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=m-1\end{matrix}\right.\)

Để biểu thức \(\sqrt{x_1}+\sqrt{x_2}=2\) xác định \(\Rightarrow x_1;x_2\ge0\Rightarrow\left\{{}\begin{matrix}x_1+x_2\ge0\\x_1x_2\ge0\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}2m\ge0\\m-1\ge0\end{matrix}\right.\) \(\Rightarrow m\ge1\)

Khi đó:

\(\sqrt{x_1}+\sqrt{x_2}=2\Leftrightarrow x_1+x_2+2\sqrt{x_1x_2}=4\)

\(\Leftrightarrow2m+2\sqrt{m-1}=4\)

\(\Leftrightarrow m+\sqrt{m-1}=2\)

Đặt \(\sqrt{m-1}=t\ge0\Rightarrow m=t^2+1\)

\(\Rightarrow t^2+1+t=2\Rightarrow t^2+t-1=0\Rightarrow\left[{}\begin{matrix}t=\dfrac{-1+\sqrt{5}}{2}\\t=\dfrac{-1-\sqrt{5}}{2}< 0\left(loại\right)\end{matrix}\right.\)

\(\Rightarrow\sqrt{m-1}=\dfrac{-1+\sqrt{5}}{2}\Rightarrow m-1=\dfrac{3-\sqrt{5}}{2}\)

\(\Rightarrow m=\dfrac{5-\sqrt{5}}{2}\)

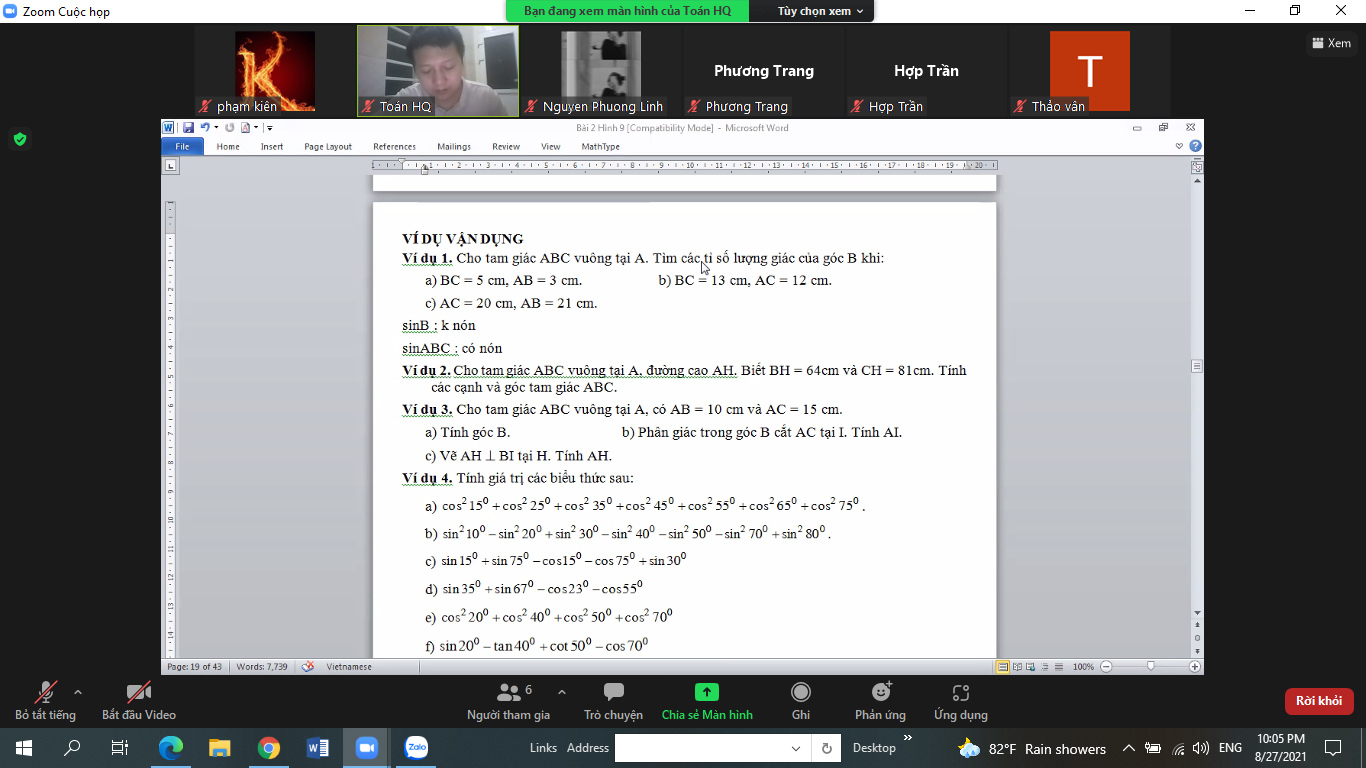
a: Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow BC^2=10^2+15^2=325\)

hay \(BC=5\sqrt{13}\left(cm\right)\)

Xét ΔBAC vuông tại A có 

\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{15}{5\sqrt{13}}=\dfrac{3}{\sqrt{13}}\)

\(\Leftrightarrow\widehat{B}\simeq56^0\)

b: Xét ΔBAC có 

BI là đường phân giác ứng với cạnh AC

nên \(\dfrac{AI}{AB}=\dfrac{CI}{BC}\)

hay \(\dfrac{AI}{10}=\dfrac{CI}{5\sqrt{13}}\)

mà AI+CI=15cm

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{AI}{10}=\dfrac{CI}{5\sqrt{13}}=\dfrac{AI+CI}{10+5\sqrt{13}}=\dfrac{15}{10+5\sqrt{13}}=\dfrac{-2+\sqrt{13}}{3}\)

Do đó: \(AI=\dfrac{-20+10\sqrt{13}}{3}\left(cm\right)\)

Cường có số thời gian rảnh rỗi là:   \(1-\frac{1}{3}-\frac{1}{6}-\frac{1}{12}-\frac{1}{8}-\frac{1}{24}=\frac{1}{4}\)

các cậu diễn giải ra đc k

a) Góc xAK kề bù với góc 115 độ nên góc xAK = 65⁰

Vì Ky song song với Ax nên góc AKy = xAk = 65⁰ ( so le trong ) 

b) Vì Ky song song với Mz nên zMK + yKM = 180⁰ ( trong cùng phía ) => góc yKM = 35⁰

=> góc AKM = AKy + yKM = 55⁰ + 35⁰ = 90⁰ hay AK vuông góc với MK

1 A

2 B

3 A

4 A

5 A

6 C

7 D

8 B

a) Thay m=3 vào hệ pt, ta được:

\(\left\{{}\begin{matrix}x+3y=3\\3x+4y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x+9y=9\\3x+4y=6\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}5y=3\\x+3y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{3}{5}\\x=3-3y=3-3\cdot\dfrac{3}{5}=\dfrac{6}{5}\end{matrix}\right.\)

Vậy: Khi m=3 thì hệ phương trình có nghiệm duy nhất là \(\left(x,y\right)=\left(\dfrac{6}{5};\dfrac{3}{5}\right)\)