hình tứ giác MNPQ có chu vi là 46dm,tổng độ dài 3 cạnh MN,NP,PQ là 30dm,hai cạnh PQ,QM là 26dm.Tính độ dài PQ

Những câu hỏi liên quan
Chu vi hình bình hành MNPQ là 56dm.Cạnh MN dài hơn cạnh NP 8 dm.Tính độ dài cạnh PQ và cạnh MQ .
Câu 1: Chu vi hình bình hành MNPQ là 56dm.Cạnh MN dài hơn cạnh NP là 8dm.Tính độ dài cạnh MN và cạnh NP
Đúng 0
Bình luận (0)
bài 1
cho hình tam abc đều,có độ dài cạnh ab bằng 6 cm.Tính độ dài đoạn tẳng bc và ca
bài 2 cho hình vuông mnpq có độ dài cạnh pq bằng 5cm.Tính độ dài các đoạn thẳng mn,np,qm
Tứ giác MNPQ có MN=NP= PQ=QM và M=90 độ khi đó MNPQ là?
Cho hình thang MNPQ ( MN//PQ, MN,PQ ). Gọi A, B, C, D lần lượt là trung điểm của MN, NP, PQ, QM
1. CMR: tứ giác ABCD là hình bình hành
2. Giả sử MQ vuông góc với NP
a) CMR: tứ giác ABCD là hình chữ nhật
b) Cho MQ= 12cm, NP= 16cm, tính độ dài AC
1: Xét ΔNMP có NA/NM=NB/NP
nên AB//MP và AB=MP/2
Xét ΔQMP có QC/QP=QD/QM
nên DC//MP và DC=MP/2
=>AB//DC và AB=DC
=>ABCD là hình bình hành
Đúng 1
Bình luận (0)
chu vi hình bình hành MNPQ là 68 dm.Cạnh MN dài hơn cạnh NP 10 cm.Tính đọ dài cạnh PQ và cạnh MQ
Cho tứ giác MNPQ. Gọi E, F , G, H lần lượt là trung điểm các cạnh MN, NP, PQ, QM. Tứ giác EFGH là hình thoi nếu 2 đường chéo MP, NQ của tứ giác MNPQ:
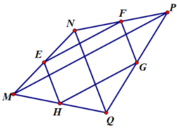
A. Bằng nhau
B. Vuông góc
C. Vuông góc với nhau tại trung điểm mỗi đường
D. Cắt nhau tại trung điểm mỗi đường.
Cho tứ giác MNPQ .Gọi E,F,G,H lần lượt là trung điểm của các cạnh MN,NP,PQ,QM. Chứng minh tứ giác EFGH là hình bình hành
cho tứ giác MNPQ, điểm A,B,C,D lần lượt là trung điểm của các cạnh MN,NP,PQ, QM. CMR tứ giác ABCD là hình bình hành
tự vẽ hình
nối MP
Xét t/g MNP có: AM=AN(gt),BN=BP(gt)
=>AB là đường tb của t/g MNP
=>AB//MP và AB=1/2MP (1)
Xét t/g MQP có: MD=DQ(gt),QC=CP(gt)
=>CD là đường tb của t/g MQP
=.CD//MP và CD=1/2MP(2)
Từ (1) và (2) => AB=CD (3)
Lại có:AB//MP, CD//MP
=>AB//CD (4)
Từ (3)và (4) => tứ giác ABCD là HBH
Đúng 0
Bình luận (0)
Cho hình chữ nhật MNPQ. Gọi AB; CD theo thứ tự là trung điểm các cạnh MN; NP; PQ; QM Chứng minh rằng: Tứ giác ABCD là hình thoi
Xét ΔMNQ có
A là trung điểm của MN
D là trung điểm của MQ
Do đó: AD là đường trung bình của ΔMNQ
Suy ra: AD//NQ và AD=NQ/2(1)
Xét ΔNPQ có
B là trung điểm của NP
C là trung điểm của QP
Do đó: BC là đường trung bình của ΔNPQ
Suy ra: BC//NQ và BC=NQ/2(2)
Từ (1) và (2) suy ra AD//BC và AD=BC
Xét ΔMNP có
A là trung điểm của MN
B là trung điểm của NP
Do đó: AB là đường trung bình của ΔMNP
Suy ra: AB=MP/2=NQ/2(3)
Từ (1) và (3) suy ra AD=AB
Xét tứ giác ABCD có
AD//BC
AD=BC
Do đó: ABCD là hình bình hành
mà AB=AD
nên ABCD là hình thoi
Đúng 0
Bình luận (0)























