Cho tam giác ABC nhọn có AB < AC. Phân giác của góc A cắt BC tại D. Trên AC lấy điểm E sao cho AE = AB.
a) Chứng minh: góc ADB = góc ADE
b) Đường thẳng ED cắt đường thẳng AB tại F. Chứng minh rằng: AF = AC.
c) Chứng minh: tam giác DBF = tam giác DEC
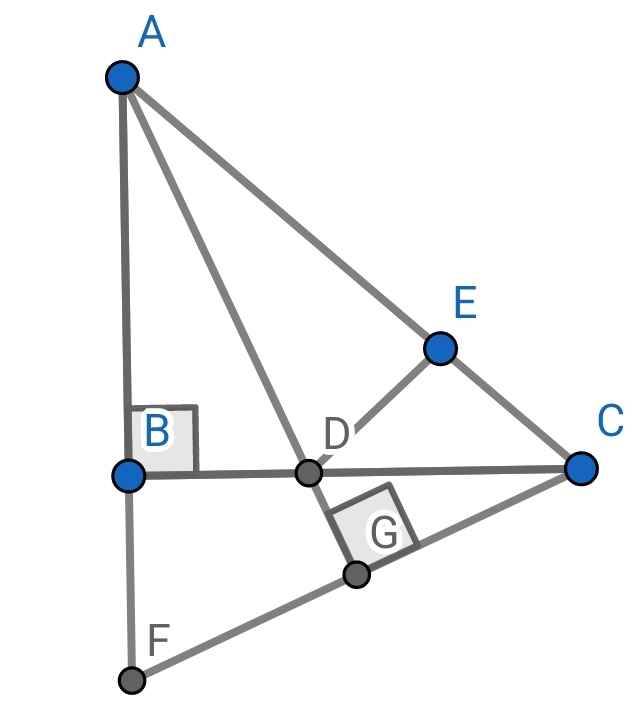
Cho tam giác ABC vuông tại A có AB < AC. Vẽ AD là tia phân giác của góc BAC (D thuộc BC). Trên AC lấy điểm E sao cho AE = AB
a, Chứng minh rằng : Tam giác ADB tam giác ADE rồi suy ra góc ABD = gócAED
b, Tia ED cắt AB tại F. Chứng minh rằng : AC = AF
c, Gọi G là trung điểm của DF; AD cắt CF tại H và cắt CG tại I. Chứng minh rằng : DI = IH
a: Xét ΔADB và ΔADE có
AD chung
góc BAD=góc EAD
AB=AE
=>ΔADB=ΔADE
=>góc ABD=góc AED
b: Xét ΔAEF vuông tại A và ΔABC vuông tại A có
AE=AB
góc AEF=góc ABC
=>ΔAEF=ΔABC
=>AC=AF
Cho tam giác ABC có AB < AC. Tia phân giác của góc A cắt BC tại D, trên tia AC lấy điểm E sao cho góc ADB = góc ADE.
a) Chứng minh tam giác ABE là tam giác cân.
b) Đường thẳng DE cắt tia AB tại F. Chứng minh tam giác AFC là tam giác cân.
c) Chứng minh BE // FC.
d) Qua C kẻ đường thẳng vuông góc với AC, qua F kẻ đường thẳng vuông góc với AF, hai đường thẳng này cắt nhau tại I. Chứng minh ba điểm A, D, I thẳng hàng.
Giúp mình với!!
Cho tam giác ABC có ba góc nhọn (AB<AC).Tia phân giác của góc BAC cắt BC tại D. Lấy điểm E trên AC sao cho AE=AB.
a) Chứng minh: tam giác ADB= tam giác ADE
b) Vẽ DH vuông góc với AB(H thuộc AB), DK vuông góc với AC (K thuộc AC).Chứng minh: BH=EK
c)Từ E vẽ đường thẳng song song với KD cắt BC tại M. Chứng minh: góc DEM= góc BDH
d) Chứng minh: góc DEM+ góc ACB=90 độ- góc CDE
cho Tam giác ABC có 3 góc nhọn (AB < AC). tia phân gics của góc BAC cắt BC tại D. Lấy E trên AC sao cho AE=AB.
a) chứng minh TG ADB= TG ADE
b) Vẽ DH vuông với AB( H thuộc AB), DK vuông với AC(K thuộc AC). chứng minh BH = EK
c) Từ E vẽ đường thẳng song song với KD cắt BC tại M. Chứng minh góc DEM = góc BDH
d) CHứng minh góc DEM + góc ACD = 90 độ - góc CDE
a: Xét ΔADB và ΔADE có
AD chung
góc BAD=góc EAD
AB=AE
=>ΔABD=ΔAED
b: Xét ΔBHD vuông tại H và ΔEKD vuông tại K có
DB=DE
góc DBH=góc DEK
=>ΔBHD=ΔEKD
=>BH=EK
c: góc DEM=góc KDE
góc KDE=góc BDH
=>góc DEM=góc BDH
d: góc DEM+góc ACD
=góc BDH+góc ACD
=90 độ-góc CDE
cho tam giác ABC vuông tại A (AB<AC) tia phân giác của góc A cắt BC tại D qua D kẻ đường thẳng vuông góc với BC cắt AC tại E trên AB lấy điểm F sao cho AF=AE chứng minh:
a) Góc B= góc DEC
b) Tam giác DBE là tam giác cân
c)Chứng minh DB=DE
Cho tam giác ABC vuông ở B, trên cạnh AC lấy điểm E sao cho AE = AB. Tia phân giác của góc A cắt BC tại D.
a, Chứng minh Δ ADB = ΔADE
b, Chứng minh DE\(\perp\)AC
c, Một đường thẳng qua C và vuông góc với AD cắt đường thẳng AB ở F. Chứng minh BF=CE
a) Xét ∆ADB và ∆ADE có:
AD chung
Góc BAD = góc EAD (AD là tia phân giác của góc BAC)
AB = AE (gt)
⇒∆ADB = ∆ADE (c-g-c)
b) Do ∆ADB = ∆ADE (c-g-c)
⇒góc ABD = góc AED (hai góc tương ứng)
⇒góc AED = 90⁰
Hay DE vuông góc AC
c) Gọi G là giao điểm của CF và AD
Do góc BAD = góc EAD (cmt)
⇒góc FAG = góc CAG
Xét hai tam giác vuông: ∆AGF và ∆AGC có:
AG chung
góc FAG = góc CAG (cmt)
⇒∆AGF = ∆AGC (cạnh góc vuông - góc nhọn kề)
⇒AF = AC (hai cạnh tương ứng)
Mà AF = AB + BF
AC = AE + EC
AB = AE
⇒BF = CE
Cho tam giác ABC (AB < AC). Tia phân giác của góc BAC cắt BC tại D. Trên cạnh AC lấy điểm E sao cho AE = AB.
a) Chứng minh: tam giác ABD = tam giác AED và góc ABD = góc DEC
b) Hai tia AB và ED cắt nhau tại F. Chứng minh: tam giác DBF = tam giác DEC
c) Đường thẳng qua E song song với AD cắt BC tại M. Gọi N là trung điểm của đoạn thẳng FC. Chứng minh rằng: DN // EM
Cho tam giác ABC vuông tại A có AB = AC Gọi I là trung điểm của BC D là trung điểm của AC a chứng minh tam giác amb bằng tam giác ABC và AE vuông góc với BC b từ A kẻ đường thẳng vuông góc với BD cắt BC tại D trên tia đối của tia de lấy điểm F sao cho de = AB Chứng minh rằng tam giác ADM bằng C D E Từ đó suy ra AE = AB song song với CD e từ C kẻ đường thẳng vuông góc với AC cắt tại g Chứng minh tam giác ABD bằng tam giác ABC Chứng minh rằng AB = ACG
Cho tam giác ABC có AB < AC. Tia phân giác của góc BAC cắt cạnh BC tại D. Trên cạnh AC lấy E sao cho AE = AB.
a) Chứng minh tam giác ABD=AED
b) Tia ED cắt AB tại F, chứng minh tam giác BDF=EDC
c) Chứng minh: BE//FC
d) Chứng minh: BD<DC
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
b: Xét ΔBDF và ΔEDC có
\(\widehat{BDF}=\widehat{EDC}\)
DB=DE
\(\widehat{DBF}=\widehat{DEC}\)
Do đó: ΔBDF=ΔEDC