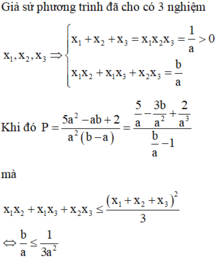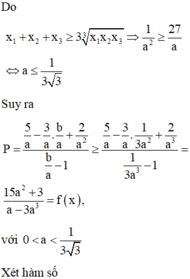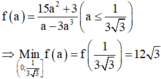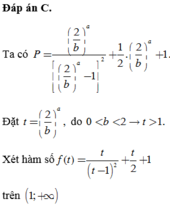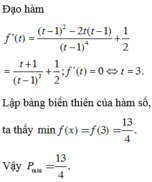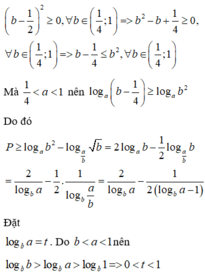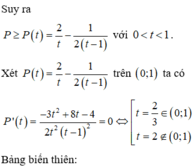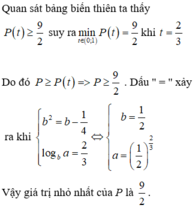cho a,b là hai số thực sao cho a*b>0 tìm giá trị nhỏ nhất của biểu thức A = (a+b)(1/a+1/b)

Những câu hỏi liên quan
Xét phương trình ax3- x2+ bx-10 với a, b là các số thực a≠0; a≠ b sao cho các nghiệm đều là số thực dương. Tìm giá trị nhỏ nhất của biểu thức
P
5
a
2
-
3
a
b
+
2
a
2
(
b
-...
Đọc tiếp
Xét phương trình ax3- x2+ bx-1=0 với a, b là các số thực a≠0; a≠ b sao cho các nghiệm đều là số thực dương. Tìm giá trị nhỏ nhất của biểu thức P = 5 a 2 - 3 a b + 2 a 2 ( b - a ) .
A. 15 3
B. 8 2
C. 11 6
D. 12 3
Giả sử phương trình đã cho có 3 nghiệm
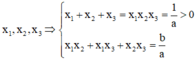
Khi đó
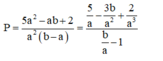
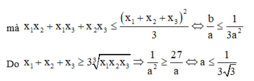
Suy ra
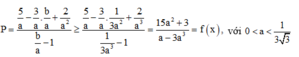
Xét hàm số:
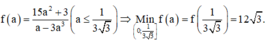
Chọn D.
Đúng 0
Bình luận (0)
Xét phương trình
a
x
3
−
x
2
+
b
x
−
1
0
với a, b là các số thực,
a
≠
0
,
a
≠
b
sao cho các nghiệm đều là số thực dương. Tìm giá trị nhỏ nhất của biểu thức
P
5
a
2...
Đọc tiếp
Xét phương trình a x 3 − x 2 + b x − 1 = 0 với a, b là các số thực, a ≠ 0 , a ≠ b sao cho các nghiệm đều là số thực dương. Tìm giá trị nhỏ nhất của biểu thức P = 5 a 2 − 3 a b + 2 a 2 b − a .
A. 15 3 .
B. 8 2 .
C. 11 6 .
D. 12 3 .
Cho a,b là hai số thực thõa mãn a.b>0
Khi đó, giá trị nhỏ nhất của biểu thức Q=(a+b)(1/a+1/b), Qmin=?
(a+b)(1/a+1/b)=1+a/b+b/a+1
=2+(a^2+b^2)/(a*b)
vì a^2+b^2>0; a*b>0
=>Qmin=2
Đúng 0
Bình luận (0)
Cho hai số thực a,b thỏa mãn a0, 0ba. Tìm giá trị nhỏ nhất của biểu thức
P
(
2
b
)
a
2
a
−
b
a
2
+...
Đọc tiếp
Cho hai số thực a,b thỏa mãn a>0, 0<b<a. Tìm giá trị nhỏ nhất của biểu thức P = ( 2 b ) a 2 a − b a 2 + 2 a + 2 b a 2 b a
A. P min = 9 4 .
B. P min = 7 4 .
C. P min = 13 4 .
D. P min = 4 .
Cho hai số thực dương a,b thỏa mãn a+b =1 . Tìm giá trị nhỏ nhất của biểu thức :
a) A = a^2 + b^2
b) B = a^2 - ab + b^2
vì (a-1)2 ≥ 0 nên a2 +1 ≥ 2a ∀mọi x (1)
vì (b-1)2 ≥ 0 nên b2 +1 ≥ 2b ∀ mọi x (2)
từ 1 và 2 ⇒ a2+b2 ≥ 2a+2b
⇒ A≥ 2(a+b)=2
dấu''=' xảy ra khi a=b=1/2
Đúng 0
Bình luận (0)
Cho hai số thực dương a; b thỏa mãn log2(a + 1) + log2(b + 1) ≥ 6 Giá trị nhỏ nhất của biểu thức S = a + b là
A.12
B.14
C. 8
D.16
Chọn B.
Ta có 6 ≤ log2(a + 1) + log2(b + 1) = log2[(a + 1)(b + 1) ]
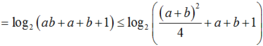
Suy ra: ![]() hay ( a + b) 2 + 4( a + b) + 4 ≥ 256
hay ( a + b) 2 + 4( a + b) + 4 ≥ 256
Tương đương: (a + b) 2 + 4(a + b) - 252 ≥ 0
Suy ra: a + b ≥ 14
Đúng 0
Bình luận (0)
Cho hai số thực a, b thỏa mãn
1
4
b
a
1
. Tìm giá trị nhỏ nhất của biểu thức
P
log
a
b
-
1
4
-
log...
Đọc tiếp
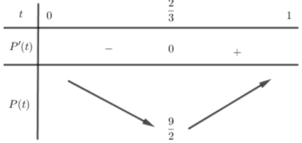
Cho hai số thực a, b thỏa mãn 1 4 < b < a < 1 . Tìm giá trị nhỏ nhất của biểu thức P = log a b - 1 4 - log a b b
A. P = 7 2
B. P = 3 2
C. P = 9 2
D. P = 1 2
Cho biết a và b là các số thực thay đổi sao cho đa thức A(x) = x^2-2ax+2a^2+b^2 - 5 có nghiệm. Hãy tìm giá trị nhỏ nhất của biểu thức P=(a+1)(b+1)
Để phương trình có nghiệm thì :
\(\Delta_x=a^2-\left(2a^2+b^2-5\right)\ge0\)
\(\Leftrightarrow a^2+b^2\le5\)
\(\Leftrightarrow\left(a+b\right)^2\le5+2ab\)
\(\Leftrightarrow ab\ge\frac{\left(a+b\right)^2-5}{2}\)
Ta có :
\(P=\left(a+1\right)\left(b+1\right)=ab+a+b+1\)
\(\ge\frac{\left(a+b\right)^2-5}{2}+\left(a+b\right)+1=\frac{1}{2}\left(a+b+1\right)^2-2\ge-2\)
Dấu " = " xảy ra khi \(\hept{\begin{cases}a=-2\\b=1\end{cases}}\)
Đúng 0
Bình luận (0)
Cho a và b là hai số thực dương thay đổi. Tìm giá trị nhỏ nhất của biểu thức: \(P=\sqrt{a+b}-\dfrac{1}{\sqrt{a+b}}+\dfrac{2015}{2014a+2006b+6\sqrt{ab}}\)