Giả sử phương trình đã cho có 3 nghiệm
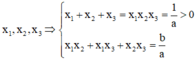
Khi đó
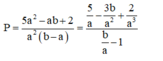
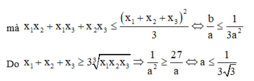
Suy ra
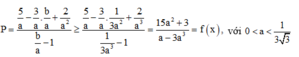
Xét hàm số:
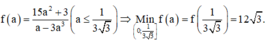
Chọn D.
Giả sử phương trình đã cho có 3 nghiệm
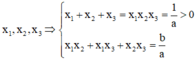
Khi đó
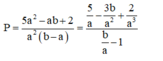
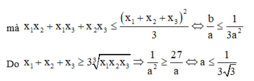
Suy ra
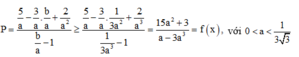
Xét hàm số:
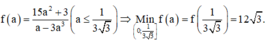
Chọn D.
Số thực m nhỏ nhất để phương trình 8 x + 3 x . 4 x + ( 3 x 2 + 1 ) 2 x = ( m 3 - 1 ) x 3 + ( m - 1 ) x có nghiệm dương là a + eln b, , với a,b là các số nguyên. Giá trị của biểu thức a + b bằng
A. 7
B. 4
C. 5
D. 3
Xét các số nguyên dương a,b sao cho phương trình a ln 2 x + b ln x + 5 = 0 có hai nghiệm phân biệt x 1 ; x 2 và phương trình 5 log 2 x + b log x + a = 0 có hai nghiệm phân biệt x 3 ; x 4 thỏa mãn x 1 x 2 > x 3 x 4 . Tìm giá trị nhỏ nhất S m i n của S = 2a+3b.
A. Smin = 25
B. Smin = 17
C. Smin = 30
D. Smin = 33
Cho hàm số f ( x ) = 3 x - 4 + ( x + 1 ) . 2 7 - x - 6 x + 3 . Giả sử m 0 = a b a , b ∈ ℤ , a b l à p h â n s ố t ố i g i ả n là giá trị nhỏ nhất của tham số thực m sao cho phương trình f 7 - 4 6 x - 9 x 2 + 2 m - 1 = 0 có số nghiệm nhiều nhất. Tính giá trị của biểu thức P = a + b 2
A. 11
B. 7
C. -1
D. 9
Cho x,y,z,a,b,c là các số thực thay đổi thỏa mãn ( x + 3 ) 2 + ( y - 2 ) 2 + ( z + 1 ) 2 = 2 và a+b+c=1. Giá trị nhỏ nhất của biểu thức P = ( x - a ) 2 + ( y - b ) 2 + ( z - c ) 2 là
A. 3 - 2
B. 3 + 2
C. 5 - 2 6
D. 5 + 2 6
Xét các số thực a; b thỏa mãn a > b > 1 Tìm giá trị nhỏ nhất Pmin của biểu thức P = log a b 2 a 2 + 3 log b a b
A.19
B.13
C.14
D.15
Xét các số thực a; b thỏa mãn a > b > 1 . Tìm giá trị nhỏ nhất của P của biểu thức P = log a b 2 a 2 + 3 log b a b
A. 19.
B. 13.
C. 14.
D. 15.
Cho a, b là các số thực và f ( x ) = a ln 2017 ( x 2 + 1 + x ) + b x sin 2018 x + 2 . Biết f ( 5 log c 6 ) = 6 , tính giá trị của biểu thức P = f ( - 6 log c 5 ) với 0 < c ≠ 1
A. P = -2
B. P = 6
C. P = 4
D. P = 2
Cho phương trình (m + 1) 16x - 2( 2m - 3) .4x + 6m + 5 = 0 với m là tham số thực. Tập tất cả các giá trị của m để phương trình có hai nghiệm trái dấu có dạng (a; b). Tính P = a.b
A. 4
B. -4
C. 5
D. -5
Cho phương trình 2 log 4 2 x 2 - x + 2 m - 4 m 2 + log 1 2 x 2 + m x - 2 m 2 = 0 . Biết rằng S = a ; b ∪ c ; d , a < b < c < d là tập hợp các giá trị của tham số m để phương trình đã cho có hai nghiệm phân biệt x1, x2 thỏa mãn x 1 2 + x 2 2 > 1 . Tính giá trị biểu thức A = a + b + 5c + 2d.
A. A = 1
B. A = 2
C. A = 0
D. A = 3