Chọn D.
Ta có:
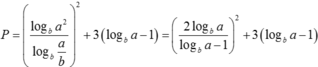
Đặt t = logba – 1 > logbb – 1 = 0; khi đó:
![]()
Ta có: ![]()
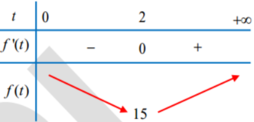
Và f’(t) = 0 khi 3t3 - 8( t + 1) = 0 hay t = 2.
Suy ra Pmin = f(2) = 15
Chọn D.
Ta có:
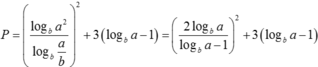
Đặt t = logba – 1 > logbb – 1 = 0; khi đó:
![]()
Ta có: ![]()
Và f’(t) = 0 khi 3t3 - 8( t + 1) = 0 hay t = 2.
Suy ra Pmin = f(2) = 15

Xét các số thực a; b thỏa mãn a > b > 1 Tìm giá trị nhỏ nhất Pmin của biểu thức P = log a b 2 a 2 + 3 log b a b
A.19
B.13
C.14
D.15
Xét các số thực a, b thỏa mãn 1 4 < b < a < 1 Biểu thức P = log a ( b - 1 4 ) - log a b b đạt giá trị nhỏ nhất khi
A. log a b = 1 3
B. log a b = 2 3
C. log a b = 3 2
D. log a b = 3
Xét các số thực a, b thỏa mãn a> b > 1. Tìm giá trị nhỏ nhất của biểu thức P = log a b 2 ( a 2 ) + 3 log b a b
A. P m i n = 19
B. P m i n = 13
C. P m i n = 14
D. P m i n = 15
Xét các số thực a; b thỏa mãn a> b> 1 . Tìm giá trị nhỏ nhất Pmin của biểu thức P = log 2 a b a 2 + 3 log b a b
A. 19
B. 13
C. 14
D. 15
cho hai số a,b là hai số thực đều lớn hơn 1. giá trị nhỏ nhất của biểu thức s=
\(\dfrac{1}{log_{b\sqrt[3]{a}}}\)+\(\dfrac{1}{log\sqrt[3]{ab^2}}\)
Giả sử a, b là các số thực sao cho x3 + y3 = a.103x + b.102x đúng với mọi số thực dương x, y, z thỏa mãn log (x + y) = z và log(x2 + y2) = z + 1. Giá trị của a+b bằng:
A. - 31 2
B. - 25 2
C. 31 2
D. 29 2
Tính giá trị của biểu thức sau: \(log^2_{\dfrac{1}{a}}a^2+log_{a^2}a^{\dfrac{1}{2}}\) (1≠a>0)
A. \(\dfrac{17}{4}\)
B. \(\dfrac{13}{4}\)
C. \(-\dfrac{11}{4}\)
D. -\(\dfrac{15}{4}\)
Xét số thực a,b thỏa mãn b > 1 và a ≤ b < a . Biểu thức P = log a b a + 2 log b a b đạt giá trị nhỏ nhất khi
A. a = b 2 .
B. a 2 = b 3 .
C. a 3 = b 2 .
D. a 2 = b .
Cho x,y,z,a,b,c là các số thực thay đổi thỏa mãn ( x + 3 ) 2 + ( y - 2 ) 2 + ( z + 1 ) 2 = 2 và a+b+c=1. Giá trị nhỏ nhất của biểu thức P = ( x - a ) 2 + ( y - b ) 2 + ( z - c ) 2 là
A. 3 - 2
B. 3 + 2
C. 5 - 2 6
D. 5 + 2 6