cho ab - cd=76 tinh 2ab-1cd
các bạn giúp tui với
Cho ab - cd = 85 . Tìm hiệu 2 số ? a ,2ab - 1cd = ? b , ab3 - cd1 = ?
cho ab-cd=76hoi2ab-1cd=
Dap an dung la
Ta co ab-cd=76 vi the 2ab-1cd se bang 176
cho hinh thang can abc day nho ab = bc dg cheo ac vuong goc ad
a) tinh cac goc hinh thang can
b) cm cd = 2ab
Giup minh vs
Vẽ hình theo yêu cầu sau:
a) Vẽ hai đường thẳng d và d’ sao cho d // d’.
b) Vẽ hai đoạn thẳng AB và CD sao cho CD = 2AB và CD //AB
a) Vẽ đường thẳng d
Vẽ đường thẳng d’ song song với d
b) Vẽ đoạn thẳng CD. Đo độ dài CD.
Kẻ đường thẳng a // CD
Trên đường thẳng a, lấy 2 điểm A và B sao cho AB = CD : 2

Chú ý:
Để dễ dàng vẽ 2 đường thẳng song song, ta có thể kẻ các đường thẳng trùng với dòng kẻ của quyển vở.
Cho hình thang cân ABCD (AB // CD); CD = 2AD = 2AB = 8. Tính diện tích của hình thang đó.
A. 12 2
B. 12 3
C. 12
D. 12 6
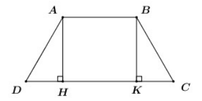
Kẻ AH, BK cùng cuông góc với CD (H, K CD)
Xét tứ giác ABKH có: A B / / H K A H / / B K , suy ra ABKH là hình bình hành.
Lại có A H K ^ = 90 0 nên ABKH là hình chữ nhật, do đó HK = AB = 4
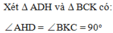
AD = BC (tính chất hình thang cân)
A D H ^ = A C K ^ = ACK (tính chất hình thang cân)
⇒ ∆ A D H = ∆ B C K (cạnh huyền – góc nhọn)
=> DH = CK (hai cạnh tương ứng)
Mà DH + CK = CD – HK = 8 – 4 = 4
Do đó DH = CK = 2
Áp dụng định lý Py-ta-go trong tam giác vuông ADH ta có:
![]()
Vậy diện tích hình thang ABCD là:

Đáp án cần chọn là: B
Cho hình thang cân ABCD là hình thang cân (AB//CD;AB<CD), biết AB=8cm, CD=2AB, AH\(⊥\)CD và AH=3cm. Khi đó chu vi hình thang cân ABCD là ....cm
cho hình thang abcd(ab//cd).m trung điểm cd.biết chu vi các tam giác amd,bmc,amb bằng nhau.cmr cd = 2ab
Cho hình thang ABCD(AB//CD) có CD=2AB. Gọi E là trung điểm CD> Chứng minh AE//BC;AD=BE
Bài làm
* Từ B kẻ đường thẳng đi qua E . Và song song với AD
Nối AE
Vì AB // CD ( gt )
=> AB // DE
=> \(\widehat{A_1}=\widehat{E_1}\)( Hai góc so le trong )
BE // AD ( cmt )
=> \(\widehat{A_2}=\widehat{E_2}\)( Hai góc so le trong )
Xét tam giác ABE và tam giác EDA có:
\(\widehat{A_1}=\widehat{E_1}\)( cmt )
Cạnh AE chung
\(\widehat{A_2}=\widehat{E_2}\)( cmt )
=> Tam giác ABE = tam giác EDA ( g.c.g )
=> AD = BE. ( hai cạnh tương ứng ) ( đpcm )
* Vì AB // CD
=> AB // EC
=> \(\widehat{B_1}=\widehat{E_3}\)( Hai góc so le trong )
Vì CD = 2AB
=> AB = CD / 2
=> AB = DE =EC
Xét tam giác AEB và tam giác BCE có:
AB = EC ( cmt )
\(\widehat{B_1}=\widehat{E_3}\)( cmt )
Cạnh BE chung
=> Tam giác AEB = tam giác BCE ( c.g.c )
=> \(\widehat{B_2}=\widehat{E_2}\)( Hai góc tương ứng )
Mà hai góc này ở vị trí so le trong
=> AE // BC ( đpcm )
# Học tốt #
cho hai cặp đoạn thẳng AB . CD và BC . AD. Biết rằng AB // CD . BC // CD. Chứng minh rằng \(AC^2+BD^2=2AB^2+2AD^2\)