Cho tứ giác ABCD có góc B = góc D =90°. Trên AC lấy 1 điểm M bất kì. MP, MQ lần lượt vuông góc với AC, AQ. Chứng minh: MP/AB + MQ/CD = 1

Những câu hỏi liên quan
tứ giác ABCD có góc D = góc B = 90 độ . Từ 1 điểm M bất kỳ trên đường chéo AC kẻ MP vuông góc với AC . MQ vuông góc với AD . C/m : MP/AB + MQ/CD = 1
Cho tam giác ABC đểu đường cao AH. Trên cạnh BC lấy điểm M bất kì (M không trùng B,C,H). Từ M kẻ MP, MQ lần lượt vuông gióc với AB,AC(P thuộc AB,Q thuộc AC)
1, Chứng minh APMQ nội tiếp
2, Gọi O là tâm đường tròn ngoại tiếp tứ giác APMQ. Chứng minh OH vuông góc với PQ
3, Chứng minh MP+MQ=AH
Cho tam giác ABC có đường cao AH .Trên cạnh BC lấy điểm M bất kì ( M không trùng với B ,C ,H ) từ M kẻ MP và MQ vuông góc với các cạnh AB ,AC
1.Chứng minh APMQ là tứ giác nội tiếp và hãy xác định tâm O của đường tròn ngoại tiếp tứ giác đó .
2.Chứng minh rằng MP+MQ=AH .
3.Chứng minh OH vuông góc với PQ.
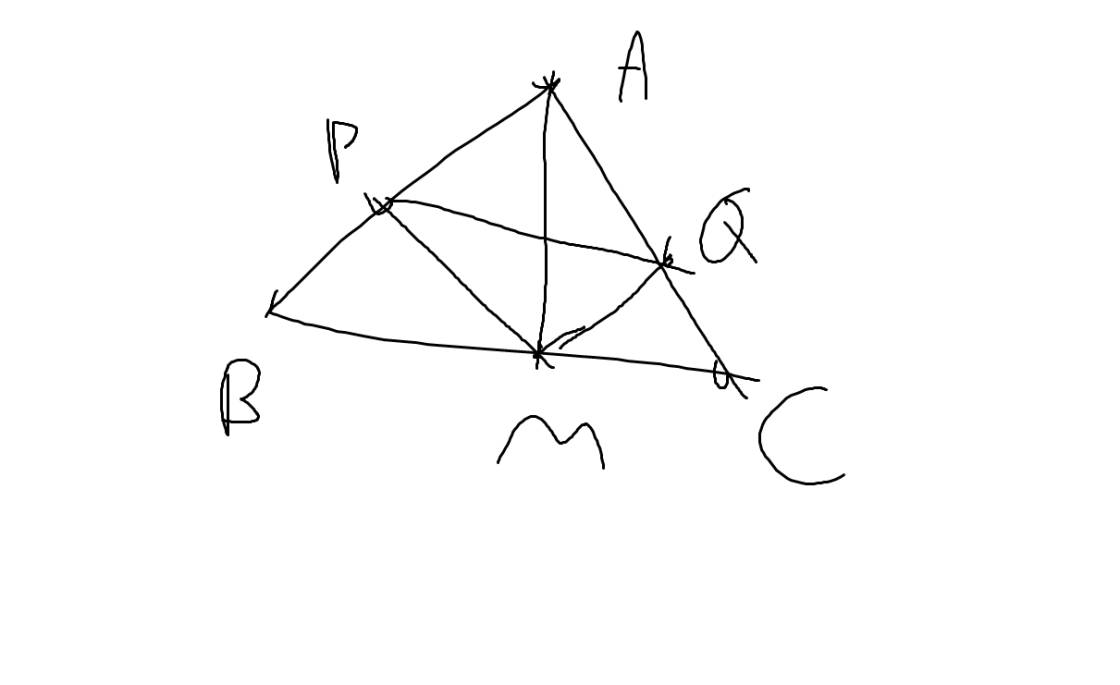
Cho tam giác ABC cân tại đỉnh A. Gọi M là trung điểm của BC. Trên cạnh AB và AC lấy các điểm P, Q sao cho MP, MQ lần lượt vuông góc với AB, AC.
Xem chi tiết
a, Chứng minh rằng MP = MQ và AP = AQ.
b, Đường thẳng PQ có vuông góc với AM không? Vì sao?
VẼ HÌNH GIÚP MÌNH NHA. CẢM ƠN Ạ
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
=>\(\widehat{BAM}=\widehat{CAM}\)
Xét ΔPAM vuông tại P và ΔQAM vuông tại Q có
AM chung
\(\widehat{PAM}=\widehat{QAM}\)
Do đó: ΔPAM=ΔQAM
=>PA=QA và MP=MQ
b: AP=AQ
=>A nằm trên đường trung trực của PQ(1)
MP=MQ
=>M nằm trên đường trung trực của PQ(2)
Từ (1) và (2) suy ra AM là đường trung trực của PQ
=>AM\(\perp\)PQ
Đúng 2
Bình luận (0)
Bài 1 :
Tam giác ABC nhọn , 2 đường cao AI , CK cắt nhay tại H biết AH = 8 cm , CH = 4cm . TÍnh độ dài 2 đường cao AI , CK khi AI + CK = 18cm
Bài 2
Tứ giác ABCD có góc B = góc D =90 độ . Từ điểm M bất kì thuôc đường chéo AC kẻ MP vuông góc với BC , MQ vuông góc với AD.
cm : \(\frac{MP}{AB}+\frac{MQ}{CD}=1\)
MONG CAO NHÂN GIẢI HỘ EM ;-;
Bài 1 : Cho tam giác ABC có góc B = góc D = 90 độ . Từ điểm M bất kì thuộc đường chéo AC kẻ MP vuông góc với BC , Mq vuông góc với AD
chứng minh : \(\frac{MP}{AB}+\frac{MQ}{CD}=1\)
Bài 2 : Tam giác ABC nhọn , 2 đường cao AI , CK cắt nhau tại H biết AH = 8 cm , CH = 4cm. Tính độ dài 2 đường cao AI , CK khi AI + CK = 18 cm
Giải hộ mình bài nào cũng được nha :3
Cho hình chữ nhật ABCD. Từ B kể BH vuông góc với AC. Gọi M,N,P,Q lần lượt là trung điểm của AH,AB,NC,DC a) Chứng minh MP=1/2 NC b) Chứng minh BM vuông góc với MQ
1)Cho tam giác đều ABC có đường cao AH. Trên cạnh BC lấy M bất kì. Từ M kẻ MP, MQ theo thứ tự vuông góc với AB, AC.
a) tìm tâm O của đường tròn ngoại tiếp tứ giác APMQ
b) CM: OH vuông góc với PQ.
2) Cho hình thang vuông( ^A=D=90o), AB=4cm, BC=13cm, CD= 9cm. Chứng minh rằng đường thẳng AD tiếp xúc với đường tròn có đường kính BC
Cho tam giác ABC đều, các đường cao AD, BH, CK của tam giác cắt nhau tại O. M là một điểm bất kì trên cạnh BC (M không trung với B, C, D) .Kẻ MP và MQ lần lượt vuông góc với AB và AC. PQ cắt OM tại R. Chứng minh rằng R la trung điểm PQ










