Cho tam giác ABC vuông tại A. BD là tia phân giác của góc ABC (D
thuộc AC). Lấy I thuộc BC sao cho BI = BA.
a. Chứng minh: ABD = IBD
b. Tính BID
c. Trên tia đối của tia AB lấy điểm K sao cho BK = BC.
Chứng minh: DK = DC

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A (AB AC). Tia phân giác của góc ABC cắt AC tại D. Trên cạnh BC lấy M sao cho BM BA.a) Chứng minh: Tam giác ABD tam giác MBDb) Chứng minh: góc MAD góc AMD c) Trên tia đối của tia AB lấy điểm E sao cho AE AB. Lấy K thuộc tia đối của tia DA sao cho KD 2DA. BD cắt KE tại H. Chứng minh H là trung điểm của KECÁC BẠN GIÚP MIK CÂU C VỚI !!! CẢM ƠN TRƯỚC NHA
Đọc tiếp
Cho tam giác ABC vuông tại A (AB < AC). Tia phân giác của góc ABC cắt AC tại D. Trên cạnh BC lấy M sao cho BM = BA.
a) Chứng minh: Tam giác ABD = tam giác MBD
b) Chứng minh: góc MAD = góc AMD
c) Trên tia đối của tia AB lấy điểm E sao cho AE = AB. Lấy K thuộc tia đối của tia DA sao cho KD = 2DA. BD cắt KE tại H. Chứng minh H là trung điểm của KE
CÁC BẠN GIÚP MIK CÂU C VỚI !!! CẢM ƠN TRƯỚC NHA
a: Xét ΔBAD và ΔBMD có
BA=BM
góc ABD=góc MBD
BD chung
=>ΔBAD=ΔBMD
b: DA=DM
=>góc DAM=góc DMA
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, BK là tia phân giác của góc ABC (K thuộc AC). Lấy điểm I thuộc BC sao cho BI = BA.
a) Kẻ AH vuông góc với BC. Chứng minh: AI là tia phân giác của góc HAC
b) Gọi E là giao điểm của AH và BK. Chứng minh tam giác AKE là tam giác cân
Có gì khong hiểu hỏi lại cj nhé:
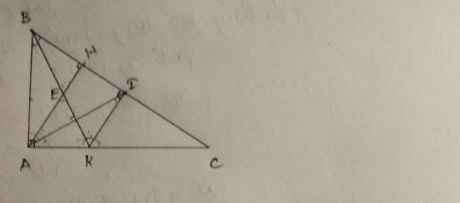
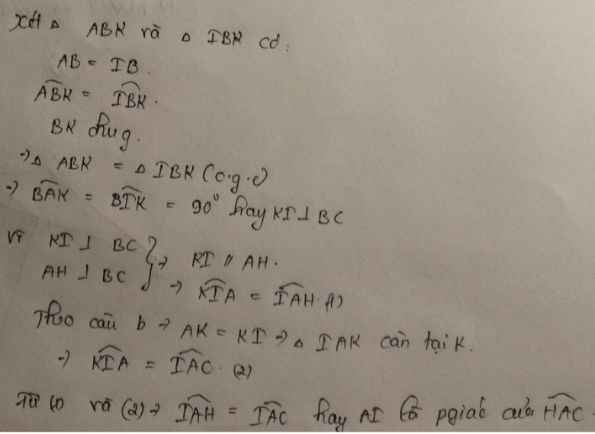
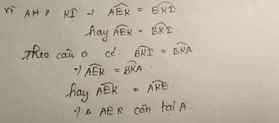
a, b ,c lần lượt từ trên xuống.
Đúng 4
Bình luận (4)
Cho tam giác ABC vuông góc tại A , kẻ BD là tia phân giác của góc ABC , ( D thuộc AC ). Trên cạnh BC lấy điểm E sao cho BEBA.a )chứng minh DE AD b.) trên tia đối của tia AB lấy điểm F sao cho AF CE chứng minh BD vuông góc EFc ) chứng minh AE //FC
Đọc tiếp
Cho tam giác ABC vuông góc tại A , kẻ BD là tia phân giác của góc ABC , ( D thuộc AC ). Trên cạnh BC lấy điểm E sao cho BE=BA.
a )chứng minh DE = AD
b.) trên tia đối của tia AB lấy điểm F sao cho AF = CE chứng minh BD vuông góc EFc ) chứng minh AE //FC
a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
Do dó: ΔBAD=ΔBED
=>DA=DE
b: Sửa đề: BD vuông góc với AE
Ta có: BA=BE
DA=DE
Do đó; BD là trung trực của AE
=>BD vuông góc với AE
c: Xét ΔBFC có BA/AF=BE/EC
nên AE//CF
Đúng 0
Bình luận (0)
Chứng minh góc ABD = góc EBD
Cho AABC vuông tại A ( AB < AC ). Tia phân giác của góc B cắt AC tại D. Trên cạnh BC lấy điem E sao cho BE= BA.
a) Chứng minh góc ABD = góc EBD
b) Chứng minh BD vuông góc AE
c) Trên tia đối của AB lấy điểm K sao cho BK= BC. Chứng minh E.D.K thăng hàng
a: \(\widehat{ABD}=\widehat{EBD}=\dfrac{\widehat{EBA}}{2}\)(vì BD là tia phân giác của góc EBA)
b: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
Suy ra: DA=DE
hay D nằm trên đường trung trực của AE(1)
Ta có: BA=BE
nên B nằm trên đường trung trực của AE(2)
Từ (1) và (2) suy ra BD⊥AE
c: Xét ΔCED vuông tại E và ΔKAD vuông tại A có
ED=AD
CE=KA
Do đó: ΔCED=ΔKAD
Suy ra: \(\widehat{CDE}=\widehat{KDA}\)
mà \(\widehat{CDE}+\widehat{EDA}=180^0\)
nên \(\widehat{EDA}+\widehat{KDA}=180^0\)
=>E,D,K thẳng hàng
Đúng 3
Bình luận (0)
Bài 5. Cho vuông tại A có AB < AC, kẻ phân giác BI của góc ABC (I Î AC). Lấy K Î BC sao cho BK = BA.
a) Chứng minh AI = KI.
b) Chứng minh AK vuông góc với BI.
c) Trên tia đối của tia AB lấy điểm E sao cho AE = KC. Chứng minh K, I, E thẳng hàng và KE = AC.
d) Chứng minh AK // EC.
a: Xét ΔBAI và ΔBKI có
BA=BK
\(\widehat{ABI}=\widehat{KBI}\)
BI chung
Do đó: ΔBAI=ΔBKI
Suy ra: AI=KI
Đúng 0
Bình luận (0)
Cho tam giác ABC có ABAC và M là trung điểm của BC. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BDCEa) Chứng minh tam giác ABM tam giác ACM từ đó suy ra AM vuông góc vs BCb) Chứng minh tam giác ABD tam giác ACE từ đó suy ra AM là tia phân giác của góc DAEc) Kẻ BK vuông góc AD( K thuộc AD) trên tia đối của tia BK lấy điểm H sao cho BHAE, trên tia đối của tia AM lấy điểm N sao cho ANCE, Chứng minh góc MAD góc MBH
Đọc tiếp
Cho tam giác ABC có AB=AC và M là trung điểm của BC. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD=CE
a) Chứng minh tam giác ABM= tam giác ACM từ đó suy ra AM vuông góc vs BC
b) Chứng minh tam giác ABD= tam giác ACE từ đó suy ra AM là tia phân giác của góc DAE
c) Kẻ BK vuông góc AD( K thuộc AD) trên tia đối của tia BK lấy điểm H sao cho BH=AE, trên tia đối của tia AM lấy điểm N sao cho AN=CE, Chứng minh góc MAD= góc MBH
Cho tam giác ABC có ABAC và M là trung điểm của BC. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BDCEa) Chứng minh tam giác ABM tam giác ACM từ đó suy ra AM vuông góc vs BCb) Chứng minh tam giác ABD tam giác ACE từ đó suy ra AM là tia phân giác của góc DAEc) Kẻ BK vuông góc AD( K thuộc AD) trên tia đối của tia BK lấy điểm H sao cho BHAE, trên tia đối của tia AM lấy điểm N sao cho ANCE, Chứng minh góc MAD góc MBHd) Chứng minh Dn vuông góc DH
Đọc tiếp
Cho tam giác ABC có AB=AC và M là trung điểm của BC. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD=CE
a) Chứng minh tam giác ABM= tam giác ACM từ đó suy ra AM vuông góc vs BC
b) Chứng minh tam giác ABD= tam giác ACE từ đó suy ra AM là tia phân giác của góc DAE
c) Kẻ BK vuông góc AD( K thuộc AD) trên tia đối của tia BK lấy điểm H sao cho BH=AE, trên tia đối của tia AM lấy điểm N sao cho AN=CE, Chứng minh góc MAD= góc MBH
d) Chứng minh Dn vuông góc DH
Cho tam giác ABC có ABAC và M là trung điểm của BC. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BDCEa) Chứng minh tam giác ABM tam giác ACM từ đó suy ra AM vuông góc vs BCb) Chứng minh tam giác ABD tam giác ACE từ đó suy ra AM là tia phân giác của góc DAEc) Kẻ BK vuông góc AD( K thuộc AD) trên tia đối của tia BK lấy điểm H sao cho BHAE, trên tia đối của tia AM lấy điểm N sao cho ANCE, Chứng minh góc MAD góc MBHd) Chứng minh Dn vuông góc DH
Đọc tiếp
Cho tam giác ABC có AB=AC và M là trung điểm của BC. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD=CE
a) Chứng minh tam giác ABM= tam giác ACM từ đó suy ra AM vuông góc vs BC
b) Chứng minh tam giác ABD= tam giác ACE từ đó suy ra AM là tia phân giác của góc DAE
c) Kẻ BK vuông góc AD( K thuộc AD) trên tia đối của tia BK lấy điểm H sao cho BH=AE, trên tia đối của tia AM lấy điểm N sao cho AN=CE, Chứng minh góc MAD= góc MBH
d) Chứng minh Dn vuông góc DH
Hình bạn tự vẽ nhé ![]()
a) Xét ΔABM và ΔACM có:
AB=AC (gt)
AM là cạnh chung
BM=CN (M là trung điểm của BC)
=> ΔABM=ΔACM (c-c-c)
=> \(\widehat{AMB}=\widehat{AMC}\) (2 góc tương ứng)
Mà ta có: \(\widehat{AMB}+\widehat{AMC}=90^o\)
=> \(\widehat{AMB}+\widehat{AMB}=180^o\)
=> \(\widehat{AMB}=90^o\)
=> AM vuông góc với BC
b) Theo câu a ta có: ΔABM=ΔACMB
=> \(\widehat{ABM}=\widehat{ACM}\)
Mà: \(\widehat{ABD}=180^o-\widehat{ABM}=180^o-\widehat{ACM}=\widehat{ACE}\)
Xét ΔABD và ΔACE có:
AB=AC (gt)
\(\widehat{ABD}=\widehat{ACE}\) (chứng minh trên)
BD=CE (gt)
=> ΔABD=ΔACE (c-g-c)
=> \(\widehat{BAD}=\widehat{CAE}\) (2 góc tương ứng)
Cũng theo câu a thì ΔABM=ΔACM
=> \(\widehat{BAM}=\widehat{CAM}\)
=> \(\widehat{BAM}+\widehat{BAD}=\widehat{CAM}+\widehat{CAE}\)
=> \(\widehat{DAM}=\widehat{EAM}\)
=> AM là tia phân giác của góc DAE
Đúng 1
Bình luận (1)
Cho tam giác ABC có ABAC và M là trung điểm của BC. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BDCEa) Chứng minh tam giác ABM tam giác ACM từ đó suy ra AM vuông góc vs BCb) Chứng minh tam giác ABD tam giác ACE từ đó suy ra AM là tia phân giác của góc DAEc) Kẻ BK vuông góc AD( K thuộc AD) trên tia đối của tia BK lấy điểm H sao cho BHAE, trên tia đối của tia AM lấy điểm N sao cho ANCE, Chứng minh góc MAD góc MBHd) Chứng minh Dn vuông góc DH
Đọc tiếp
Cho tam giác ABC có AB=AC và M là trung điểm của BC. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD=CE
a) Chứng minh tam giác ABM= tam giác ACM từ đó suy ra AM vuông góc vs BC
b) Chứng minh tam giác ABD= tam giác ACE từ đó suy ra AM là tia phân giác của góc DAE
c) Kẻ BK vuông góc AD( K thuộc AD) trên tia đối của tia BK lấy điểm H sao cho BH=AE, trên tia đối của tia AM lấy điểm N sao cho AN=CE, Chứng minh góc MAD= góc MBH
d) Chứng minh Dn vuông góc DH
a, xét tam giác AMB và tam giác AMC có : AM chung
BM = CM do M là trung điểm của BC (gt)
AB = AC (gt)
=> tam giác AMB = tam giác AMC (c-c-c)
=> góc AMB = góc AMC (đn)
mà góc AMB + góc AMC = 180 (kb)
=> góc AMB = 90
=> AM _|_ BC (đn)
b, góc ABC = góc ACB do tam giác ABC cân tại A (gt)
góc ABC + góc ABD = 180 (kb)
góc ACB + góc ACE = 180 (kb)
=> góc ABD = góc ACE
xét tam giác ABD và tam giác ACE có : BD = CE (gt)
AB = AC (gt)
=> tam giác ABD = tam giác ACE (c-g-c)
















