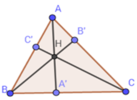
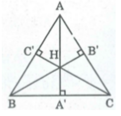
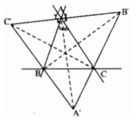
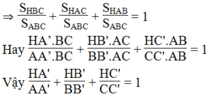cho tam giác ABC ba đường cao AA' ; BB' ; CC' gặp nhau tại H . Gọi H1;H2;H3 lần lượt là điểm đối xứng của H qua BC ; AC và AB.
a) tính tổng HA'/AA' + HB'/BB' + HC'/CC' và tổng AH1/AA' + BH2/BB'+ CH3/CC'
b) gọi I;E;F lần lượt là trung điểm của AH;BC;AC . Các đường trung trực của BC và AC cắt nhau tại O .Chứng minh : tứ giác AIEO là hình bình hành
c) các tia AO;BO;CO cắt BC;AC;AB tại A1;B1;C1. chứng minh rằng P= OA/OA1 + OB/OB1 + OC/OC1 >= 6
BAI NAY MINH LAM DUOC PHAN a .MONG CAC BAN GIUP MINH PHAN b ; c