Ta có: S H B C + S H A C + S H A B = S A B C
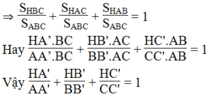

Ta có: S H B C + S H A C + S H A B = S A B C
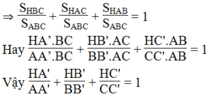
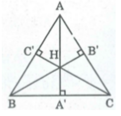
Cho tam giác ABC có ba đường cao \(AA^,,BB^,,CC^,\).Gọi H là trực tâm của tam giác đó.
a) Chứng minh \(\frac{HA^,}{AA^,}+\frac{HB^,}{BB^,}+\frac{HC^,}{CC^,}=1\)
b) Chứng minh \(\frac{AA^,}{HA^,}+\frac{BB^,}{HB^,}+\frac{CC^,}{HC^,}\ge9\)
cho tam giác ABC nhọn, các đường cao AA', BB', CC', H là trực tâm
a) tính tổng HA'/AA' + HB'/BB' + HC'/CC'
b) gọi AI là phân giác của tam giác ABC; IM, IN thứ tự là phân giác của góc AIC và góc AIB. Chứng minh rằng: AN.BI.CM = BN.IC.AM
Cho tam giác ABC nhọn. Các đường cao AA’ , BB’ , CC’. Gọi H là trực tâm.
a) Tính tổng HA’/AA’+HB’/BB’+HC’/CC’
b) Gọi AI là phân giác của tam giác ABC; IM, IN lần lượt là phân giác của góc AIC và góc AIB. Chứng minh rằng: AN.BI.CM=BN.IC.AM
c) Chứng minh rằng: (AB+BC+CA)^2/(AA’^2 +BB’^2+CC’^2) lớn hơn hoặc bằng 4
Cho tam giác ABC với ba đường cao A A ’ , B B ’ , C C ’ . Gọi H là trực tâm của tam giác đó. Chọn câu đúng
A. H A ' A A ' + H B ' B B ' + H C ' C C ' = 1
B. H A ' A A ' + H B ' B B ' + H C ' C C ' = 2
C. H A ' A A ' + H B ' B B ' + H C ' C C ' = 3
D. H A ' A A ' + H B ' B B ' + H C ' C C ' = 4
Cho tam giác ABC nhọn, các đường cao AA', BB', CC', H là trực tâm
a) Tính tổng \(\frac{HA'}{AA'}+\frac{HB'}{BB'}+\frac{HC'}{CC'}\)
b) Gọi AI là phân giác của tam giác ABC; IM, IN lần lượt là phân giác của góc AIC và AIB. Chứng minh rằng: AN.BI.CM=BN.IC.AM
c) Chứng minh rằng \(\frac{\left(AB+BC+CA\right)^2}{AA'^2+BB'^2+CC'^2}\ge4\)
Cho tam giác ABC nhọn có các đường cao AA',BB',CC' và H là trực tâm
a,chứng minh BC'.BA+CB'.CA=BC^2
b,chứng minh rằng: HB.HC/AB.AC+HA.HB/BC.AC+HC.HA/BC.AB=1
c,Gọi D là trung điểm của BC.Qua H kẻ đường thẳng vuông góc với DH cắt AB,AC lần lượt tại M,N.Chứng minh:H là trung điểm của MN
Cho tam giác ABC nhọn có các đường cao AA',BB',CC' và H là trực tâm
a,chứng minh BC'.BA+CB'.CA=BC^2
b,chứng minh rằng: HB.HC/AB.AC+HA.HB/BC.AC+HC.HA/BC.AB=1
c,Gọi D là trung điểm của BC.Qua H kẻ đường thẳng vuông góc với DH cắt AB,AC lần lượt tại M,N.Chứng minh:H là trung điểm của MN
Cho tam giác ABC nhọn, các đường cao AA', BB', CC', H là trực tâm.
a) Tính tổng HA'/AA' + HB'/BB' + HC'/CC'
b) Gọi AI là phân giác của tam giác ABC (I nằm trong ABC); IM, IN thứ tự là phân giác của góc AIC và góc AIB. Chứng minh rằng: AN.BI.CM = BN.CI.AM
c) Tam giác ABC như thế nào thì biểu thức \(\frac{\left(AB+BC+CA\right)^2}{AA'^2+BB'^2+CC'^2}\) đạt giá trị nhỏ nhất?
Cho tam giác ABC nhọn, các đường cao AA', BB', CC' và trực tâm H.
a) Tính HA'/AA'+HB'/BB'+HC'/CC'
b) Gọi AI, IM, IN là phân giác của các góc BAC, AIC và AIB. Chứng minh AN.BI.CM=BN.IC.AM
c) Chứng minh \(\frac{\left(AB+BC+CA\right)^2}{AA'^2+BB'^2+CC'^2}\ge4\)