Tìm nghiệm của phương trình sau : 2x - y = 3

Những câu hỏi liên quan
Tìm nghiệm của phương trình sau : 2x - y = 3
PT có vô số nghiệm. Bạn cần bổ sung thêm điều kiện gì thì mới giải được chứ.
Đúng 0
Bình luận (0)
Tìm nghiệm nguyên của phương trình sau
x^2y+x^2=x^3-y+2x+7
Ta có phương trình :
\(x^2y+x^2=x^3-y+2x+7\)
\(\Leftrightarrow x^2y+y=x^3-x^2+2x+7\)
\(\Leftrightarrow y.\left(x^2+1\right)=x^3-x^2+2x+7\)
\(\Leftrightarrow y=\frac{x^3-x^2+2x+7}{x^2+1}\)
Do \(y\inℤ\rightarrow\frac{x^3-x^2+2x+7}{x^2+1}\inℤ\). Lại có \(x\inℤ\Rightarrow\hept{\begin{cases}x^3-x^2+2x+7\inℤ\\x^2+1\inℤ\end{cases}}\)
\(\Rightarrow x^3-x^2+2x+7⋮x^2+1\)
\(\Leftrightarrow x.\left(x^2+1\right)-\left(x^2+1\right)+x+8⋮x^2+1\)
\(\Leftrightarrow x+8⋮x^2+1\)
\(\Rightarrow\left(x+8\right)\left(x-8\right)⋮x^2+1\)
\(\Leftrightarrow x^2+1-65⋮x^2+1\)
\(\Leftrightarrow65⋮x^2+1\)\(\Leftrightarrow x^2+1\inƯ\left(65\right)\). Mà : \(x^2+1\ge1\forall x\)
\(\Rightarrow x^2+1\in\left\{1,5,13,65\right\}\)
\(\Leftrightarrow x^2\in\left\{0,4,12,64\right\}\). \(x^2\) là số chính phương với \(x\inℤ\)
\(\Rightarrow x^2\in\left\{0,4,64\right\}\Rightarrow x\in\left\{0,2,-2,8,-8\right\}\)
+) Với \(x=0\) thì \(y=7\) ( Thỏa mãn )
+) Với \(x=2\) thì \(y=3\) ( Thỏa mãn )
+) Với \(x=-2\) thì \(y=-\frac{9}{5}\) ( Loại )
+) Với \(x=8\) thì \(y=\frac{471}{65}\) ( Loại )
+) Với \(x=-8\) thì \(y=-9\) ( Thỏa mãn )
Vậy phương trình đã cho có nghiệm \(\left(x,y\right)\in\left\{\left(-8,-9\right);\left(0,7\right);\left(2,3\right)\right\}\)
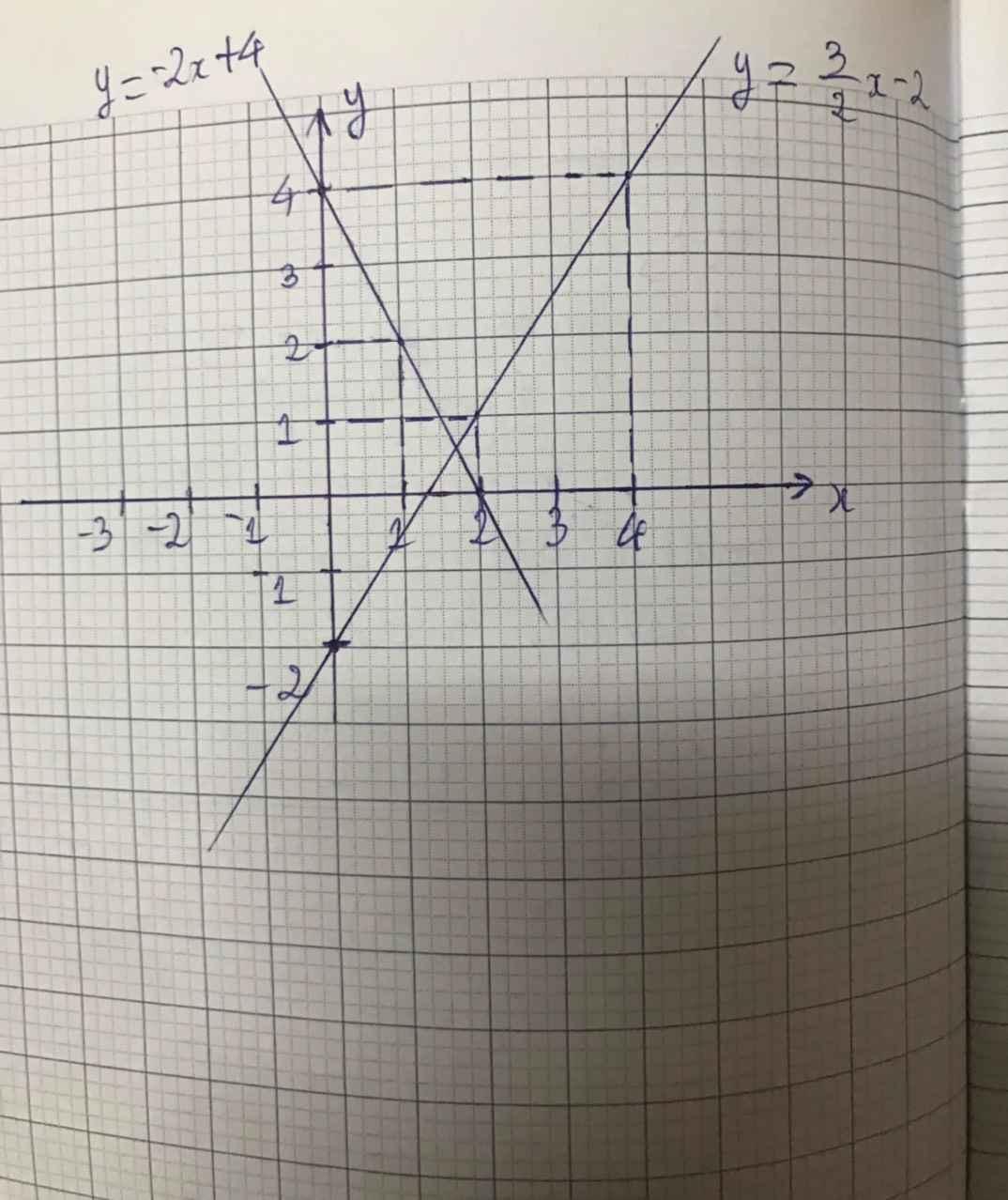
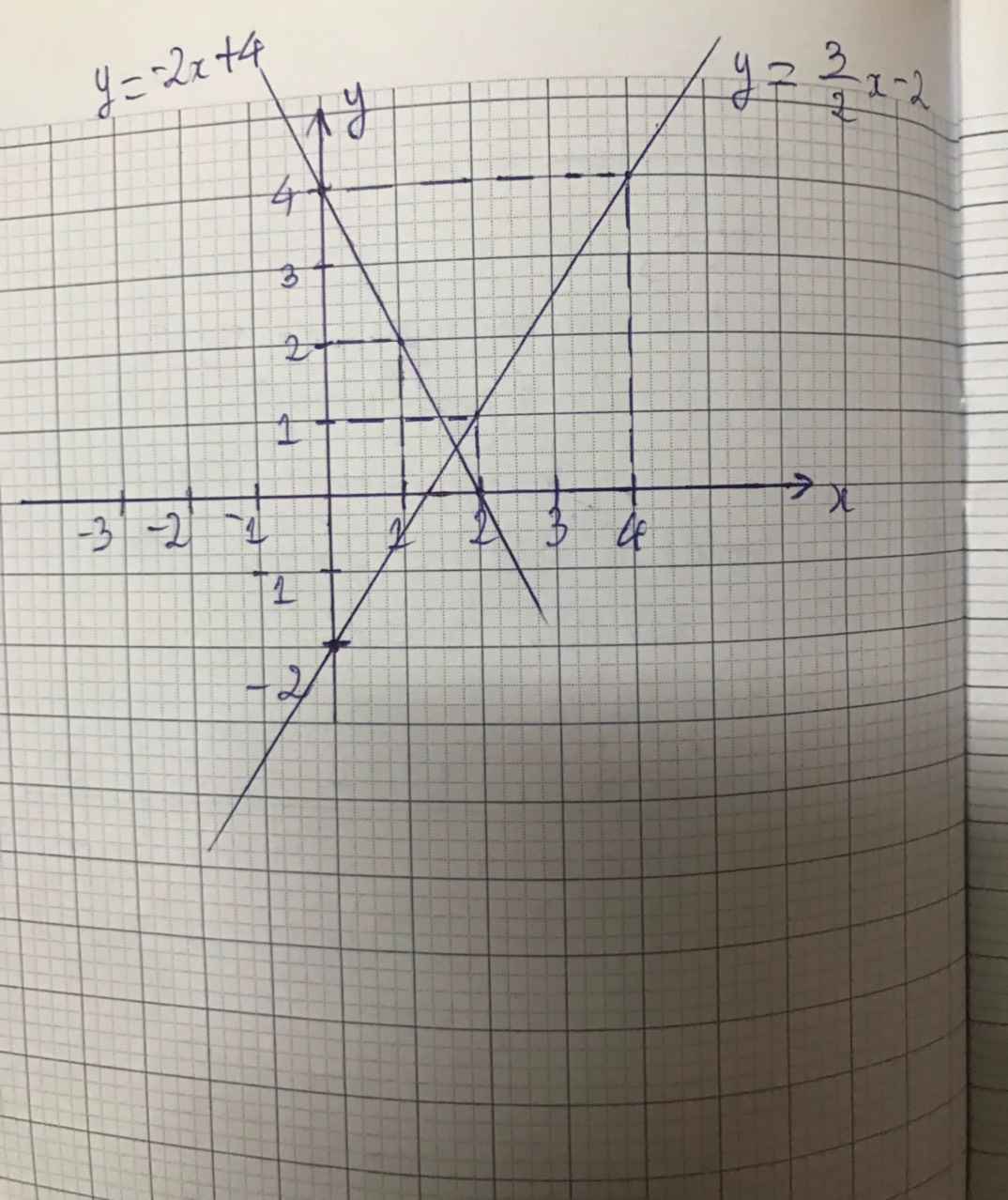
Với mỗi phương trình sau, tìm nghiệm tổng quát của phương trình và vẽ hai đường thẳng biểu diễn tập nghiệm của hai phương trình đó trên cùng một hệ toạ độ. Xác định toạ độ giao điểm của hai đường thẳng
2x + y = 3
x-2y = 4
bạn ưi, cho gửi lại tại vì hơi bị lộn kiến thức :)
tìm nghiệm tổng quát:
2x+y=4⇔x=2-1/2y hay y=4-2x
⇔y∈R ⇔ x∈R
x=2-1/2y y=4-2x
3x-2y=4⇔x=4/3+2/3yhay y=3/2x-2
⇔y∈R hay ⇔x∈R
x=4/3+2/3y y=3/2x-2
còn biểu diễn 2 cái đấy trên trục tọa độ thì mik làm r
Đúng 0
Bình luận (0)
Tìm tổng các nghiệm của phương trình sau:
log
5
4
x
2
−
2
x
−
3
2
log
2
x
2
−
2
x
−...
Đọc tiếp
Tìm tổng các nghiệm của phương trình sau:
log 5 4 x 2 − 2 x − 3 = 2 log 2 x 2 − 2 x − 4
A. 0
B. -1
C. 2
D. 3
Đáp án C
Phương pháp:
Biến đổi phương trình đã cho về 2 log 5 x 2 − 2 x − 3 = log 2 x 2 − 2 x − 4 và đặt ẩn phụ t = log 5 x 2 − 2 x − 3 đưa về phương trình ẩn t.
Xét hàm f t và tìm nghiệm của f t = 0 từ đó tìm ra nghiệm của phương trình.
Cách giải:
Phương trình (1): log 5 x 2 − 2 x − 3 = 2 log 2 x 2 − 2 x − 4
Điều kiện: x 2 − 2 x − 3 > 0 x 2 − 2 x − 4 > 0 ⇔ x 2 − 2 x − 4 > 0
Vì x 2 − 2 x − < x 2 − 2 x − 3 , ∀ x ∈ R
1 ⇔ 2 log 5 x 2 − 2 x − 3 = log 2 x 2 − 2 x − 4 *
Đặt t = log 5 x 2 − 2 x − 3
⇒ x 2 − 2 x − 3 = 5 t ⇒ x 2 − 2 x − 4 = 5 t − 1 > 0 ⇔ t > 0
Phương trình (*) trở thành:
2 t = log 2 5 t − 1 ⇔ 5 t − 4 t − 1 = 0
Xét hàm số y t = 5 t − 4 t − 1 trên 0 ; + ∞
Có y ' t = 5 t ln 5 − 4 t ln 4
Vì 5 t > 4 t , ∀ t ∈ 0 ; + ∞ ; ln 5 > ln 4 nên y t = 5 t ln − 4 t ln > 0 , ∀ t ∈ 0 ; + ∞
⇒ f t đồng biến trên 0 ; + ∞
Bảng biến thiên:

Mà f t = 0 ⇒ t = 1 là nghiệm duy nhất phương trình f t = 0
Với t = 1 ⇒ log 5 x 2 − 2 x − 3 = 1
⇔ x 2 − 2 x − 3 = 5 ⇔ x 2 − 2 x − 8 = 0
Theo định lý vi – et ta có tổng hai nghiệm phương trình (1) là: x 1 + x 2 = 2.
Chú ý khi giải:
HS cần chú ý sử dụng phương pháp xét tính đơn điệu của hàm số để giải phương trình.
Đúng 0
Bình luận (0)
Tìm số nghiệm của phương trình sau 2 x − 3 = 4 x 2 − 15
A. 1 nghiệm duy nhất
B. vô nghiệm
C. 3 nghiệm
D. 5 nghiệm
ĐKXĐ: 2 x − 3 ≥ 0 4 x 2 − 15 ≥ 0 ( * )
Với điều kiện (*) phương trình tương đương với
( 2 x − 3 ) 2 = ( 4 x 2 − 15 ) 2 ⇔ 2 x − 3 = 4 x 2 − 15
⇔ 4 x 2 − 2 x − 12 = 0 ⇔ x = 2 x = − 3 2
Thay vào điều kiện (*) ta thấy chỉ có x = 2 thỏa mãn
Vậy phương trình có nghiệm duy nhất x = 2
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Tìm nghiệm nguyên dương của phương trình sau:
(2x + 5y + 1)(2|x| + y + x2 + x) = 105
Do VP là số lẻ
<=> 2x + 5y + 1 là số lẻ và \(2^{\left|x\right|}+y+x^2+x\) là số lẻ
<=> y chẵn và \(2^{\left|x\right|}+y+x\left(x+1\right)\) là số lẻ
=> \(2^{\left|x\right|}\) là số lẻ (do y chẵn và x(x+1) chẵn)
=> x = 0
PT <=> \(\left(5y+1\right)\left(1+y\right)=105\)
<=> y = 4 (thử lại -> thỏa mãn)
KL: x = 0; y = 4
Đúng 2
Bình luận (1)
tìm nghiệm nguyên của phương trình 2x^3 -x^2y + 3x^2 +2x -y=2
2x3-x2y+3x2+2x-y=2
(2x3+2x)-(x2y+y)+(3x2+3)=5
2x(x2+1)-y(x2+1)+3(x2+1)=5
(x2+1)(2x-y+3)=5
Mà x2>=0 => x2+1>0
=> (x2+1)(2x-y+3)=5=1.5=5.1
•x2+1=1 và 2x-y+3=5 => x=0; y=-2
•x2+1=5 và 2x-y+3=1=> x=2;y=6 hoặc x=-2; y=-2
Vậy (x;y) là (0;-2);(2;6);(-2;-2)
Đúng 0
Bình luận (0)
Tìm nghiệm của phương trình 2x6+y2+2x3y=64
nghiệm nguyên
<=> y2 + 2x3y + 2x6 - 64 = 0 (1)
Coi (1) là phương trình bậc 2 ẩn y, x là tham số
(1) có nghiệm <=> Δ ≥ 0 <=> ( 2x3 )2 - 4( 1 + 2x6 - 64 ) ≥ 0
<=> 4x6 - 4 - 8x6 + 256 ≥ 0 <=> -4x6 + 252 ≥ 0 <=> x ∈ { -1 ; 0 ; 1 } ( giải bpt này khó v nên cho nghiệm luôn )
+) Với x = -1 (1) trở thành y2 - 2y - 62 = 0 có Δ = 252 không là SCP nên không có nghiệm nguyên
+) Với x = 0 (1) trở thành y2 - 64 = 0 <=> y = ±8 (tm)
+) Với x = 1 (1) trở thành y2 + 2y - 62 = 0 có Δ = 252 không là SCP nên không có nghiệm nguyên
Vậy ( x ; y ) ∈ { ( 0 ; 8 ) , ( 0 ; -8 ) }
Cho phương trình: \(x^2-3y^2+2xy-2x-10y+4\)
a) Tìm nghiệm \(\left(x;y\right)\) của phương trình thỏa mãn: \(x^2+y^2=10\)
b) Tìm nghiệm nguyên của phương trình đã cho