\(Ba\rightarrow Ba^{2+}+2e\\ K\rightarrow K^++e\\ O+2e\rightarrow O^{2-}\\ N\rightarrow N^{5+}+5e\)

b. nhé

đề như này không cụ thể khó làm lắm em ạ

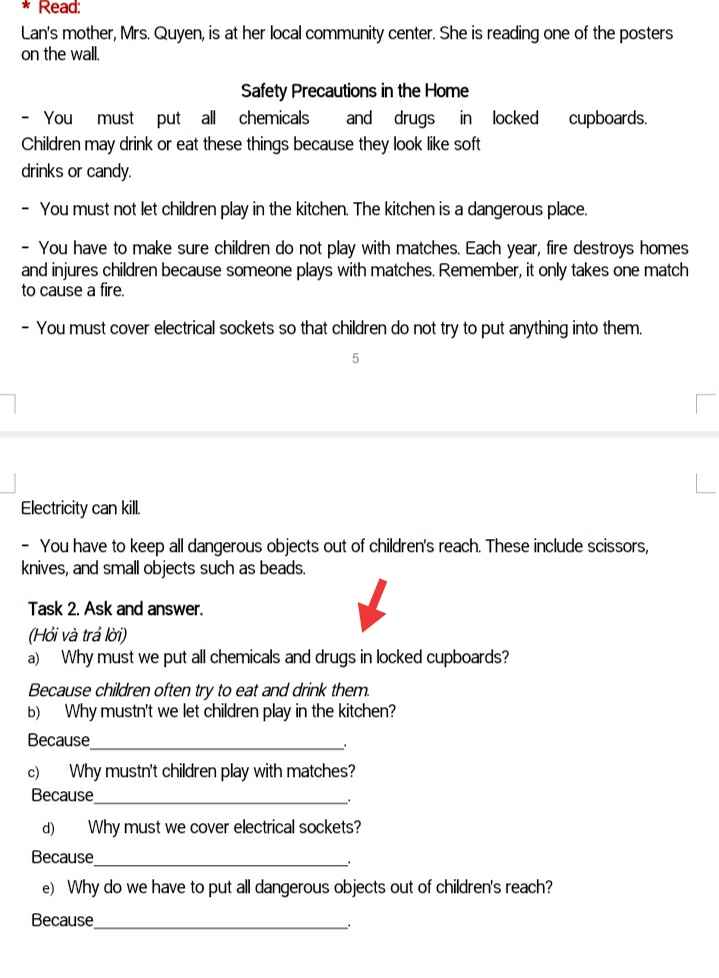
b. Because the kitchen is a dangerous place.

c. Because it only takes one match to cause a fire.

d. Because we electricity can kill.

e. Because we want to keep our children safe. (?)

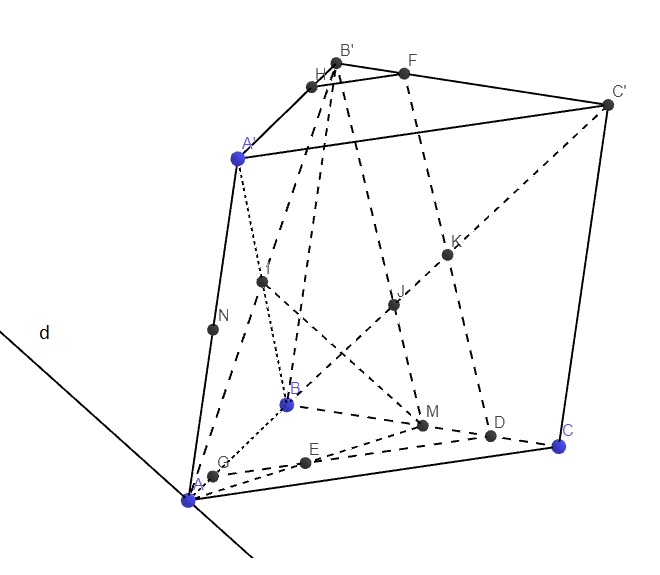
a.

Trong tam giác A'BC ta có: I là trung điểm BA', M là trung điểm BC

\(\Rightarrow IM\) là đường trung bình tam giác A'BC

\(\Rightarrow IM||A'C\)

\(\Rightarrow IM||\left(ACC'A'\right)\)

Do \(A\in\left(AB'M\right)\cap\left(ACC'A'\right)\) và \(\left\{{}\begin{matrix}IM\in\left(AB'M\right)\\A'C\in\left(ACC'A'\right)\\IM||A'C\end{matrix}\right.\)

\(\Rightarrow\) Giao tuyến của (AB'M) và (ACC'A') là đường thẳng qua A và song song A'C

Qua A kẻ đường thẳng d song song A'C

\(\Rightarrow d=\left(AB'M\right)\cap\left(ACC'A'\right)\)

b.

I là trung điểm AB', E là trung điểm AM

\(\Rightarrow IE\) là đường trung bình tam giác AB'M \(\Rightarrow IE||B'M\) (1)

Tương tự ta có IN là đường trung bình tam giác AA'B' \(\Rightarrow IN||A'B'\) (2)

(1);(2) \(\Rightarrow\left(EIN\right)||\left(A'B'M\right)\)

c.

Trong mp (BCC'B'), qua K kẻ đường thẳng song song B'M lần lượt cắt BC và B'C' tại D và F

\(DF||B'M\Rightarrow DF||IE\Rightarrow DF\subset\left(EIK\right)\)

Trong mp (ABC), nối DE kéo dài cắt AB tại G

\(\Rightarrow G\in\left(EIK\right)\)

Trong mp (A'B'C'), qua F kẻ đường thẳng song song A'C' cắt A'B' tại H

Do IK là đường trung bình tam giác A'BC' \(\Rightarrow IK||A'B'\)

\(\Rightarrow FH||IK\Rightarrow H\in\left(EIK\right)\)

\(\Rightarrow\) Tứ giác DFHG là thiết diện (EIK) và lăng trụ

Gọi J là giao điểm BK và B'M \(\Rightarrow J\) là trọng tâm tam giác B'BC

\(\Rightarrow\dfrac{BJ}{BK}=\dfrac{2}{3}\)

Áp dụng talet: \(\dfrac{BM}{BD}=\dfrac{BJ}{BK}=\dfrac{2}{3}\Rightarrow BD=\dfrac{3}{2}BM=\dfrac{3}{2}.\dfrac{1}{2}BC=\dfrac{3}{4}BC\)

\(\Rightarrow MD=\dfrac{1}{4}BC=\dfrac{1}{2}CM\Rightarrow D\) là trung điểm CM

\(\Rightarrow DE\) là đường trung bình tam giác ACM

\(\Rightarrow DE||AC\Rightarrow DE||FH\)

\(\Rightarrow\) Thiết diện là hình thang