Cho a/a'=b/b'=c/c'.tính giá trị biểu thức:(a-3b+2c)/(a'-3b'+2c')

Những câu hỏi liên quan
a. Cho a/a'=b/b'=c/c'=4.Hãy tính giá trị biểu thức a - 3b +2c/a' -3b + 2c'
Cho a, b, c là ba số dương thỏa mãn: \(\dfrac{\text{2b+c-a}}{a}=\dfrac{\text{2c-b+a}}{b}=\dfrac{\text{ 2a+b-c}}{c}\)
Tính giá trị biểu thức: P = \(\dfrac{\left(3a-2b\right)\left(3b-2c\right)\left(3a-2c\right)}{\left(3a-c\right)\left(3b-a\right)\left(3c-b\right)} \)
Vì \(a,b,c>0\Rightarrow a+b+c\ne0\)
Áp dụng tc dtsbn:
\(\dfrac{2b+c-a}{a}=\dfrac{2c-b+a}{b}=\dfrac{2a+b-c}{c}=\dfrac{2\left(a+b+c\right)}{a+b+c}=2\\ \Rightarrow\left\{{}\begin{matrix}2b+c-a=2a\\2c-b+a=2b\\2a+b-c=2c\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}3a-2b=c\\3b-2c=a\\3c-2a=b\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}3a-c=2b\\3b-a=2c\\3c-b=2a\end{matrix}\right.\\ \Rightarrow P=\dfrac{abc}{2a\cdot2b\cdot2c}=\dfrac{1}{8}\)
Đúng 0
Bình luận (0)
Cho a/a'=b/b'=c/c'=-4 và a'-3b'+2c' khác 0
Tính giá trị biểu thức : -a+3b-2c
a'-3b'+2c'
\(\frac{a}{a^,}=\frac{b}{b^,}=\frac{c}{c^,}=-4\Rightarrow\)\(\frac{-a}{a^,}=\frac{-b}{b^,}=\frac{-c}{c^,}=\frac{-a+3b-2c}{a^,-3b^,+2c^,}=4\)
Vậy
\(\frac{-a+3b-2c}{a^,-3b^,+2c^,}=4\)
Đúng 0
Bình luận (0)
cho a,b,c là 3 số dương thỏa mãn : 3a-b /c = 3b - c /a = 3c -a / b
tính giá trị biểu thức A= a/2b-3c + b/2c-3a + c/2a-3b
Cho a/b=b/c=c/a và a+b+c khác 0. Tính giá trị của biểu thức P=a^3b^2c^2003/b^2008
Cho 2a=3b=4c và a,b,c khác 0. Tìm giá trị biểu thức của A=\(\dfrac{a+b-c}{a+2b-2c}\)
\(2a=3b=4c\\ \Leftrightarrow\dfrac{a}{6}=\dfrac{b}{4}=\dfrac{c}{3}=\dfrac{2b}{8}=\dfrac{2c}{6}=\dfrac{a+b-c}{7}=\dfrac{a+2b-2c}{8}\\ \Leftrightarrow A=\dfrac{a+b-c}{a+2b-2c}=\dfrac{7}{8}\)
Đúng 2
Bình luận (0)
Cho ba số thực dương a,b,c thỏa mãn ab+bc+ca = 3abc. Tìm giá
trị lớn nhất của biểu thức T = \(\sqrt{\dfrac{a}{3b^2c^2+abc}}+\sqrt{\dfrac{b}{3b^2c^2+abc}}+\sqrt{\dfrac{c}{3a^2b^2+abc}}\)
Ta có \(ab+bc+ca=3abc\)
\(\Leftrightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=3\)
Đặt \(x=\dfrac{1}{a},y=\dfrac{1}{b},z=\dfrac{1}{c}\) thì ta có \(x,y,z>0;x+y+z=3\) và
\(\sqrt{\dfrac{a}{3b^2c^2+abc}}=\sqrt{\dfrac{\dfrac{1}{x}}{3.\dfrac{1}{y^2z^2}+\dfrac{1}{xyz}}}=\sqrt{\dfrac{\dfrac{1}{x}}{\dfrac{3x+yz}{xy^2z^2}}}=\sqrt{\dfrac{y^2z^2}{3x+yz}}\) \(=\dfrac{yz}{\sqrt{3x+yz}}\) \(=\dfrac{yz}{\sqrt{x\left(x+y+z\right)+yz}}\) \(=\dfrac{yz}{\sqrt{\left(x+y\right)\left(x+z\right)}}\)
Do đó \(T=\dfrac{yz}{\sqrt{\left(x+y\right)\left(x+z\right)}}+\dfrac{zx}{\sqrt{\left(y+z\right)\left(y+x\right)}}+\dfrac{xy}{\sqrt{\left(z+x\right)\left(z+y\right)}}\)
Lại có \(\dfrac{yz}{\sqrt{\left(x+y\right)\left(x+z\right)}}\le\dfrac{yz}{2\left(x+y\right)}+\dfrac{yz}{2\left(x+z\right)}\)
Lập 2 BĐT tương tự rồi cộng theo vế, ta được \(T\le\dfrac{yz}{2\left(x+y\right)}+\dfrac{yz}{2\left(x+z\right)}+\dfrac{zx}{2\left(y+z\right)}+\dfrac{zx}{2\left(y+x\right)}\) \(+\dfrac{xy}{2\left(z+x\right)}+\dfrac{xy}{2\left(z+y\right)}\)
\(T\le\dfrac{yz+zx}{2\left(x+y\right)}+\dfrac{xy+zx}{2\left(y+z\right)}+\dfrac{xy+yz}{2\left(z+x\right)}\)
\(T\le\dfrac{x+y+z}{2}\) (do \(x+y+z=3\))
\(T\le\dfrac{3}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow x=y=z=1\) \(\Leftrightarrow a=b=c=1\)
Vậy \(maxT=\dfrac{3}{2}\), xảy ra khi \(a=b=c=1\)
(Mình muốn gửi lời cảm ơn tới bạn Nguyễn Đức Trí vì ý tưởng của bài này chính là bài mình vừa hỏi lúc nãy trên diễn đàn. Cảm ơn bạn Trí rất nhiều vì đã giúp mình có được lời giải này.)
Đúng 2
Bình luận (0)
Bạn Lê Song Phương xem lại dùm nhé, thanks!
\(...\dfrac{yz}{\sqrt[]{\left(x+y\right)\left(x+z\right)}}\le\dfrac{2yz}{x+y}+\dfrac{2yz}{x+z}\)
\(...\Rightarrow T\le2.3=6\)
\(\Rightarrow GTLN\left(T\right)=6\left(tạia=b=c=1\right)\)
Đúng 0
Bình luận (0)
Lúc mình đọc lời giải kia của bạn thì mình thấy cũng hợp lí nhưng mà Cô-si hơi nhầm tí ở chỗ \(\dfrac{1}{z+x}+\dfrac{1}{z+y}\ge\dfrac{1}{2}.\dfrac{1}{\sqrt{\left(z+x\right)\left(z+y\right)}}\) ấy.

Nên là mình cũng dựa trên ý tưởng của bạn nhưng sửa \(\dfrac{1}{2}\) thành 2 thì mới đúng được
Không thì bạn cứ kiểm tra bằng cách thay điểm rơi \(a=b=c=1\) vào T thì nó ra \(\dfrac{3}{2}\) ngay chứ không ra 6 đâu.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho ba số thức a,b,c thỏa mãn 8(a+b+c)^3=(2a+b-c)^3+(2b+c-a)^3+(2c+b-a)^3
tính giá trị biểu thức p=(a+3b)(b+3c)(c+3a)
Sai đề! Sửa: that 2c+b-a=2c+a-b
Đặt 2a+b-c=x, 2b+c-a=y, 2c+a-b=z
\(\Rightarrow8\left(a+b+c\right)^3=\left(x+y+z\right)^3=x^3+y^3+z^3\)và \(P=\left(x+y\right)\left(y+z\right)\left(x+z\right)\)
Ta có: \(\left(x+y+z\right)^3-x^3-y^3-z^3=0\Leftrightarrow\left(x+y\right)^3+3\left(x+y\right)z\left(x+y+z\right)-x^3-y^3=0\)
\(\Leftrightarrow3xy\left(x+y\right)+3\left(x+y\right)z\left(x+y+z\right)=0\Leftrightarrow3\left(x+y\right)\left(xy+xz+yz+z^2\right)=0\)
\(\Leftrightarrow3\left(x+y\right)\left(y+z\right)\left(z+x\right)=0\Leftrightarrow3P=0\Leftrightarrow P=0\)
Đúng 0
Bình luận (0)
Cho hàm số
y
a
x
+
b
x
+
c
có đồ thị như hình vẽ, a, b, c là các số nguyên. Tính giá trị của biểu thức T a – 3b + 2c A. T – 9 B. T – 7 C. T 12 D. T 10
Đọc tiếp
Cho hàm số y = a x + b x + c có đồ thị như hình vẽ, a, b, c là các số nguyên. Tính giá trị của biểu thức T = a – 3b + 2c
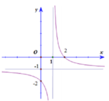
A. T = – 9
B. T = – 7
C. T = 12
D. T = 10
Đáp án A
Phương pháp: Dựa vào các đường tiệm cận và các điểm đi qua của đồ thị hàm số.
Cách giải:
Đồ thị hàm số y = a x + b x + c có đường TCĐ x = – c => – c = 1 <=> c = – 1, TCN y = a => a = –1
Đồ thị hàm số đi qua (0;–1)
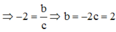
![]()
Đúng 0
Bình luận (0)



















