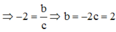
Đáp án A
Phương pháp: Dựa vào các đường tiệm cận và các điểm đi qua của đồ thị hàm số.
Cách giải:
Đồ thị hàm số y = a x + b x + c có đường TCĐ x = – c => – c = 1 <=> c = – 1, TCN y = a => a = –1
Đồ thị hàm số đi qua (0;–1)
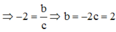
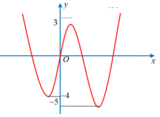
Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Biết S là tập các giá trị thực của m để hàm số y = 2 f ( x ) + m có 5 điểm cực trị. Gọi a, b lần lượt là giá trị nguyên âm lớn nhất và giá trị nguyên dương nhỏ nhất của tập S. Tính tổng T = a + b.
A. T = 2
B. T = 1
C. T = -1
D. T = -2
Cho hàm số y = f x có đồ thị như hình vẽ bên. Biết rằng tập hợp các giá trị của m để phương trình f 2 sin x = f m có 12 nghiệm phân biệt thuộc đoạn − π ; 2 π là một khoảng a ; b . Tính giá trị của biểu thức T = a 2 + b 2
A. 5
B. 4
C. 10
D. 13
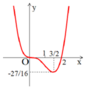
Cho hàm số y = x − a b x + c có đồ thị như hình vẽ bên. Tính giá trị của biểu thức P=a+b+c
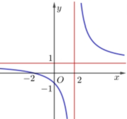
A. P = - 3
B. P = 1
C. P = 5
D. P = 2
Cho hàm số y = f(x) có đồ thị như hình bên. Biết S là tập các giá trị thực của m để hàm số y = 2 f x + m có 5 điểm cực trị. Gọi a, b lần lượt là giá trị nguyên âm lớn nhất và giá trị nguyên dương nhỏ nhất của tập S. Tổng T=a+b là
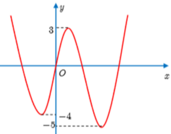
A. 2
B. 1
C. -1
D. 3
Ta xác định được các số a, b, c để đồ thị hàm số y = x 3 + a x 2 + b x + c đi qua điểm (0;1) và có điểm cực trị (-2;0). Tính giá trị của biểu thức T=4a+b+c?
A. 20
B. 23
C. 24
D. 22
Cho hàm số y = a x - 1 b x + c có đồ thị như dưới đây. Tính giá trị biểu thức T = a + 2 b + 3 c
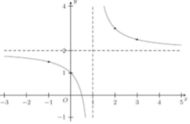
A. T = 1.
B. T = 2.
C. T = 3.
D. T = 4.
Biết đồ thị hàm số y = x 3 + a x 2 + b x + c (với a, b, c là các số thực(đi qua điểm (1;0) và có điểm cực trị (-2; 0) . Tính giá trị biểu thức T = a 2 + b 2 + c 2 + 2 .
A. 18
B. 7
C. 9
D. 27
Cho các số thực a, b, c, d thỏa mãn 0 < a < b < c < d và hàm số y = f(x). Biết hàm số y = f'(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y = f(x) trên [ 0 ; d ] . Khẳng định nào sau đây là khẳng định đúng?
A. M + m = f(b) + f(a)
B. M + m = f(d) + f(c)
C. M + m = f(0) + f(c)
D. M + m = f(0) + f(a)
Cho hai hàm số y=f(x) và y=g(x) là hai hàm số liên tục trên ℝ có đồ thị hàm số y=f’(x) là đường cong nét đậm, đồ thị hàm số y=g’(x) là đường cong nét mảnh như hình vẽ. Gọi ba giao điểm A, B, C của y=f’(x) và y=g’(x) trên hình vẽ lần lượt có hoành độ là a, b, c. Tìm giá trị nhỏ nhất của hàm số h(x)=f(x)-g(x) trên đoạn [a;c]
A. m i n h x a ; c = h 0
B. m i n h x a ; c = h a
C. m i n h x a ; c = h b
D. m i n h x a ; c = h c
