Chọn D.
Phương pháp: Sử dụng các tính chất hàm số đa thức bậc 3.

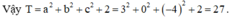
Chọn D.
Phương pháp: Sử dụng các tính chất hàm số đa thức bậc 3.

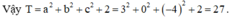
Cho hàm số y = a x − 4 x + b có đồ thị C . Đồ thị C nhận đường thẳng x = 2 làm tiệm cận đứng và C . đi qua điểm A 4 ; 2 . Tính giá trị của biểu thức P = a + b .
A. P = 0.
B. P = − 8.
C. P = 3.
D. P = 5.
Cho hàm số y = f ( x ) = x 3 – ( 2 m - 1 ) x 2 + ( 2 - m ) x + 2 . Tập tất cả các giá trị của m để đồ thị hàm số y = f x có 5 điểm cực trị là a b ; c với a, b, c là các số nguyên và a b là phân số tối giản. Tính a+b+c
A. 11
B. 8
C. 10
D. 5
Ta xác định được các số a, b, c để đồ thị hàm số y = x 3 + a x 2 + b x + c đi qua điểm (0;1) và có điểm cực trị (-2;0). Tính giá trị của biểu thức T=4a+b+c?
A. 20
B. 23
C. 24
D. 22
Cho hàm số y = f x = a x 3 + b x 2 + c x + d có đồ thị (C). Biết đồ thị hàm số (C) có hai điểm cực trị A(2;-27) ; B(-4;81). Tính S=-a+b-c+d
A. S = 24
B. S = 27
C. S = 31
D. S = 32
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d (a;b;c;d ∈ R, a ≠ 0) có đồ thị (C). Biết rằng đồ thị (C) đi qua gốc tọa độ và có đồ thị hàm số y = f’(x) cho bởi hình vẽ sau đây.

Tính giá trị H = f(4) – f(2)
A. H = 51
B. H = 54
C. H = 58
D. H = 64
Cho hàm số y = x + b a x − 2 có đồ thị là (C). Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của (C) tại điểm M 1 ; − 2 song song với đường thẳng 3 x + y − 4 = 0. Khi đó tổng giá trị của a + b bằng:
A. 2
B. 1
C. -1
D. 0
Cho hàm số f ( x ) = x 3 + 3 a x 2 + 3 x + 3 có đồ thị (C) và g ( x ) = x 3 + 3 b x 2 + 9 x + 5 có đồ thị (H), với a, b lá các tham số thực. Đồ thị (C), (H) có chung ít nhất 1 điểm cực trị. Tìm giá trị nhỏ nhất của biểu thức P = a + 2 b
A. 21 .
B. 2 6 + 6.
C. 3 + 5 3 .
D. 2 6 .
Cho hàm số y = f x = x 3 - 2 m - 1 x 2 + 2 - m x + 2 . Tập tất cả các giá trị của m để đồ thị hàm số y = f x có 5 điểm cực trị là a b ; c với a, b, c là các số nguyên và a b là phân số tối giản. Tính a + b + c
A. a + b + c = 11
B. a + b + c = 8
C. a + b + c = 10
D. a + b + c = 5
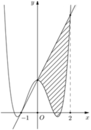
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại 2 điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳng x=0, x=2 có diện tích bằng 28 5 (phần gạch chéo trong hình vẽ)
A. 2 5
B. 1 9
C. 2 9
D. 1 5