Giải giúp mình với đang cần gấp lắm rồi 🙏🙏🙏

Những câu hỏi liên quan
Giải phương trình: a) √2x - 2 + 2√(2x - 3) + √2x + 13 + 3√(2x - 3) = 5. Giúp mình với mình đang cần rất gấp ạ🙏🙏🙏🙏
Giúp mình với ạ, mình đang cần gấp deadline còn nửa tiếng hơn nữa thôi ạ. Lập dàn ý thôi ạ🙏🙏🙏🙏
Mn giúp đỡ mình với ạ
Mình đang cần gấp lắm ạ🙏
Giúp em bài 5 với ạ. Cần gấp lắm. Em cảm ơn ạ 🙏🙏🙏🙏🙏😭😭
5:
a: sin x=2*cosx
\(A=\dfrac{6cosx+2cosx-4\cdot8\cdot cos^3x}{cos^3x-2cosx}\)
\(=\dfrac{8-32cos^2x}{cos^2x-2}\)
b: VT=sin^4(pi/2-x)+cos^4(x+pi/2)+6*1/2*sin^22x+1/2*cos4x
=cos^4x+sin^4x+3*sin^2(2x)+1/2*(1-2*sin^2(2x))
=1-2*sin^2x*cos^2x+3*sin^2(2x)+1/2-sin^2(2x)
==3/2=VP
Đúng 0
Bình luận (0)
a+1/a-1=? (a=x/y)
Help me giúp mình với đang cần gấp🥺🥺🥺🥺🥺🙏🙏🥺🥺🥺🙏🙏
Tìm số nguyên n để 3n+2 chia hết cho n-1
Giúp mình đi mình cần gấp lắm 🙏🙏🙏🙏😭😭
3n+2 \(⋮\)n-1
=> 3n+1 \(⋮\)n-1
=> (3n +1) - 3(n-1)
=> (3n+1) - ( 3n-3)
=> 3n+1 -3n+3
=> ( 3n-3n) + (1+3)
=> 4 \(⋮\)n-1
=> n-1 \(\in\)Ư(4)= { 1;2 ;4; -1; -2; -4}
Xong bn tự thay nha
Mk ko biết trình bày cho lắm
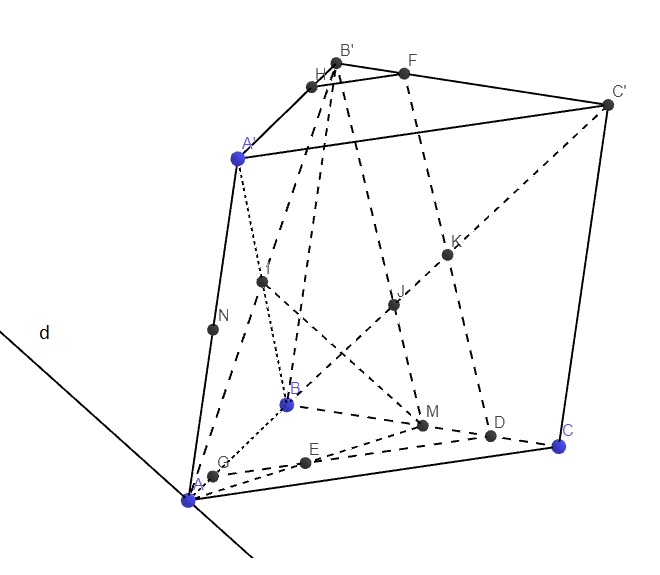
Giúp em câu 4 với ạ. Cần gấp lắm ạ😢😢🙏🙏🙏
a.
Trong tam giác A'BC ta có: I là trung điểm BA', M là trung điểm BC
\(\Rightarrow IM\) là đường trung bình tam giác A'BC
\(\Rightarrow IM||A'C\)
\(\Rightarrow IM||\left(ACC'A'\right)\)
Do \(A\in\left(AB'M\right)\cap\left(ACC'A'\right)\) và \(\left\{{}\begin{matrix}IM\in\left(AB'M\right)\\A'C\in\left(ACC'A'\right)\\IM||A'C\end{matrix}\right.\)
\(\Rightarrow\) Giao tuyến của (AB'M) và (ACC'A') là đường thẳng qua A và song song A'C
Qua A kẻ đường thẳng d song song A'C
\(\Rightarrow d=\left(AB'M\right)\cap\left(ACC'A'\right)\)
b.
I là trung điểm AB', E là trung điểm AM
\(\Rightarrow IE\) là đường trung bình tam giác AB'M \(\Rightarrow IE||B'M\) (1)
Tương tự ta có IN là đường trung bình tam giác AA'B' \(\Rightarrow IN||A'B'\) (2)
(1);(2) \(\Rightarrow\left(EIN\right)||\left(A'B'M\right)\)
Đúng 0
Bình luận (0)
c.
Trong mp (BCC'B'), qua K kẻ đường thẳng song song B'M lần lượt cắt BC và B'C' tại D và F
\(DF||B'M\Rightarrow DF||IE\Rightarrow DF\subset\left(EIK\right)\)
Trong mp (ABC), nối DE kéo dài cắt AB tại G
\(\Rightarrow G\in\left(EIK\right)\)
Trong mp (A'B'C'), qua F kẻ đường thẳng song song A'C' cắt A'B' tại H
Do IK là đường trung bình tam giác A'BC' \(\Rightarrow IK||A'B'\)
\(\Rightarrow FH||IK\Rightarrow H\in\left(EIK\right)\)
\(\Rightarrow\) Tứ giác DFHG là thiết diện (EIK) và lăng trụ
Gọi J là giao điểm BK và B'M \(\Rightarrow J\) là trọng tâm tam giác B'BC
\(\Rightarrow\dfrac{BJ}{BK}=\dfrac{2}{3}\)
Áp dụng talet: \(\dfrac{BM}{BD}=\dfrac{BJ}{BK}=\dfrac{2}{3}\Rightarrow BD=\dfrac{3}{2}BM=\dfrac{3}{2}.\dfrac{1}{2}BC=\dfrac{3}{4}BC\)
\(\Rightarrow MD=\dfrac{1}{4}BC=\dfrac{1}{2}CM\Rightarrow D\) là trung điểm CM
\(\Rightarrow DE\) là đường trung bình tam giác ACM
\(\Rightarrow DE||AC\Rightarrow DE||FH\)
\(\Rightarrow\) Thiết diện là hình thang
Đúng 0
Bình luận (0)
Bài này mình cần gấp lắm rồi xin hãy giúp mình 🙏 
a) Xét ΔNMD và ΔNED có
NM=NE(gt)
\(\widehat{MND}=\widehat{END}\)(ND là tia phân giác của \(\widehat{NME}\))
ND chung
Do đó: ΔNMD=ΔNED(c-g-c)
Suy ra: \(\widehat{NMD}=\widehat{NED}\)(hai góc tương ứng)
mà \(\widehat{NMD}=90^0\)(gt)
nên \(\widehat{NED}=90^0\)
hay DE\(\perp\)NP
b) Ta có: NM=NE(gt)
nên N nằm trên đường trung trực của ME(1)
Ta có: DM=DE(ΔNMD=ΔNED)
nên D nằm trên đường trung trực của ME(2)
Từ (1) và (2) suy ra ND là đường trung trực của ME
Đúng 2
Bình luận (1)
Tìm hiểu một số ứng dụng của "Đội hình đội ngũ" trong cuộc sống hằng ngày .
🙏Mình đang cần gấp các bạn giải nhanh giúp mình với nhé 🙏
Mình sẽ giúp bạn nêu một số ứng dụng của “đội hình đội ngũ” trong cuộc sống hằng ngày, dễ hiểu và gần gũi: 🌟 Ứng dụng của “đội hình đội ngũ” 1. Trong nhà trường Khi xếp hàng vào lớp, ra về, tập thể dục giữa giờ, chào cờ,… giúp học sinh đi lại trật tự, nhanh gọn. Tạo thói quen kỷ luật, gọn gàng. 2. Trong quân đội, công an Rèn luyện tính tổ chức, kỷ luật, phối hợp tập thể. Dùng trong duyệt binh, lễ chào cờ, di chuyển lực lượng. 3. Trong thể thao Một số môn cần đội hình rõ ràng: bóng đá (hàng thủ, hàng công), bóng chuyền (vị trí chuyền 1, 2, 3...), điền kinh tiếp sức (đứng theo hàng). Giúp phân công nhiệm vụ và phối hợp hiệu quả. 4. Trong lao động, sản xuất Xếp hàng để nhận đồ ăn, mua vé, đi siêu thị, đi thang máy,… đều áp dụng nguyên tắc đội hình đội ngũ. Trong xây dựng, sản xuất: công nhân làm việc theo nhóm, đứng theo hàng để dễ phân công và an toàn. 5. Trong sinh hoạt cộng đồng Khi tham gia lễ hội, diễu hành, văn nghệ, đồng diễn thể dục thể thao,… đội hình đội ngũ tạo sự đẹp mắt, đồng đều. Tóm lại: “Đội hình đội ngũ” rèn cho con người tính kỷ luật, sự ngăn nắp, tinh thần tập thể và được ứng dụng ở trường học, quân đội, thể thao, lao động, sinh hoạt cộng đồng.
Đúng 0
Bình luận (0)