Tìm x thuộc z ,biết:
1+ -1/60+19/120<x/36+ -1/60<58/90+59/72+ -1/60
tìm x thuộc z biết 1 + 1/60 + 19/120 < x/36 + -1/60 < 58/90 + 59/72 + -1/60
Tìm x thuộc Z, biết: \(1+\frac{-1}{60}+\frac{19}{120}
tìm x thuộc z biết 1 +\(\frac{1}{60}\)+ \(\frac{19}{120}< \frac{x}{36}+\frac{-1}{60}< \frac{58}{90}+\frac{59}{72}+\frac{-1}{60}\)
Bài 1:Cho p/s
A= n + 1/n + 2
Tìm n thuộc Z để A có GT nguyên âm, dương
Bài 2: Tìm x thuộc Z
1 + (-1/60) + 19/120 < x/36 + (-1/60) < 58/90 + 59/72 + (-1/60)
Hép mi vs nào ace!!
Bài 1 :
\(A=\dfrac{n+1}{n+2}\) có giá trị nguyên âm, dương khi
\(n+1⋮n+2\)
\(\Rightarrow n+1-\left(n+2\right)⋮n+2\)
\(\Rightarrow n+1-n-2⋮n+2\)
\(\Rightarrow-1⋮n+2\)
\(\Rightarrow n+2\in\left\{-1;1\right\}\)
\(\Rightarrow n\in\left\{-3;-1\right\}\left(n\in Z\right)\)
Bài 2 :
\(1+\left(-\dfrac{1}{60}\right)+\dfrac{19}{120}< \dfrac{x}{36}+\left(-\dfrac{1}{60}\right)< \dfrac{58}{90}+\dfrac{59}{72}+\left(-\dfrac{1}{60}\right)\)
\(\Rightarrow1+\dfrac{19}{120}< \dfrac{x}{36}< \dfrac{58}{90}+\dfrac{59}{72}\)
\(\Rightarrow\dfrac{139}{120}< \dfrac{x}{36}< \dfrac{232}{360}+\dfrac{295}{360}\)
\(\Rightarrow\dfrac{417}{360}< \dfrac{10x}{360}< \dfrac{527}{360}\)
\(\Rightarrow417< 10x< 527\)
\(\Rightarrow10x\in\left\{420;430;440;450;460;470;480;490;500;510;520\right\}\)
\(\Rightarrow x\in\left\{42;43;44;45;46;47;48;49;50;51;52\right\}\)
Ta có : = = 1 +
a, A có giá trị nguyên khi n + 1 chia hết cho n - 2 ⇔ 3 chia hết cho n - 2
⇒ n - 2 ∈ Ư ( 3 ) = { ± 1 ; ± 3 }
⇒ n ∈ { 1 ; 3 ; - 1 ; 5 }
Bài 2:
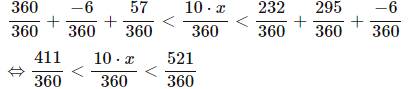
\(\text{Vậy tập hợp giá trị của x là:}\) 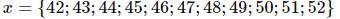
tìm x, biết: 1+-1/60+19/120<x/36<58/90+59/72+-1/60
tìm x biết :
1+\(\dfrac{-1}{60}\)+\(\dfrac{19}{120}\)<\(\dfrac{x}{36}\)<\(\dfrac{58}{90}\)+\(\dfrac{59}{72}\)+\(\dfrac{-1}{60}\)
tìm x biết
1+ -1/60+19/120<x/36<58/90+59/72+ -1/60
Số giá trị x∈Z , thỏa mãn 1+\(\dfrac{-1}{60}\)+\(\dfrac{19}{120}\)<\(\dfrac{x}{36}\)+\(\dfrac{-1}{60}\)<\(\dfrac{58}{90}\)+\(\dfrac{59}{72}\)+\(\dfrac{-1}{60}\) là :
tìm \(x\in Z\)
\(1+\frac{-1}{60}+\frac{19}{120}<\frac{x}{36}+\frac{-1}{60}<\frac{58}{90}+\frac{59}{72}+\frac{-1}{60}\)