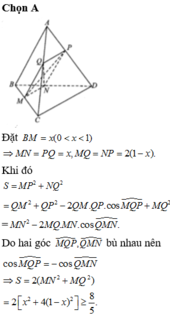
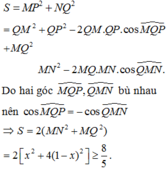Cho Hình vuông ABCD cạnh a. M là trung điểm của AB . Tính giá trị biểu thức : (AB +AD)(BD+BC)

Những câu hỏi liên quan
Cho hình vuông ABCD cạnh a. M là trung điểm của AB, Tính giá trị các biểu thức sau:
(
A
B
→
+
A
D
→
)
.
(
B
D
→
+
B
C
→
)
A. a2 B. –a2 C. 2a2 D. Đáp á...
Đọc tiếp
Cho hình vuông ABCD cạnh a. M là trung điểm của AB, Tính giá trị các biểu thức sau: ( A B → + A D → ) . ( B D → + B C → )
A. a2
B. –a2
C. 2a2
D. Đáp án khác
Chọn A.
Theo quy tắc hình bình hành ta có ![]()
Do đó
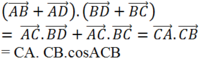
(![]() vì AC và BD vuông góc với nhau)
vì AC và BD vuông góc với nhau)
Mặt khác ![]() và theo định lý Pitago ta có:
và theo định lý Pitago ta có:
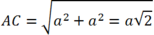
Suy ra ![]()
![]()
Đúng 0
Bình luận (0)
Cho hình vuông ABCD cạnh a . Tính giá trị các biểu thức sau:
a) overrightarrow{AB}.overrightarrow{AC}
b)left(overrightarrow{AB}+overrightarrow{AD}right)left(overrightarrow{BD}+overrightarrow{BC}right)
c)overrightarrow{AB}.overrightarrow{BD}
d) left(overrightarrow{AC}-overrightarrow{AB}right)left(2overrightarrow{AD}-overrightarrow{AB}right)
e) left(overrightarrow{AB}+overrightarrow{AC}+overrightarrow{AD}right)left(overrightarrow{DA}+overrightarrow{DB}+overrightarrow{DC}right)
Đọc tiếp
Cho hình vuông ABCD cạnh a . Tính giá trị các biểu thức sau:
a) \(\overrightarrow{AB}.\overrightarrow{AC}\)
b)\(\left(\overrightarrow{AB}+\overrightarrow{AD}\right)\left(\overrightarrow{BD}+\overrightarrow{BC}\right)\)
c)\(\overrightarrow{AB}.\overrightarrow{BD}\)
d) \(\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\left(2\overrightarrow{AD}-\overrightarrow{AB}\right)\)
e) \(\left(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}\right)\left(\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{DC}\right)\)
a, \(AC=\dfrac{AB}{sin45^o}=\dfrac{a}{\dfrac{\sqrt{2}}{2}}=a\sqrt{2}\)
\(\overrightarrow{AB}.\overrightarrow{AC}=AB.AC.cos\widehat{BAC}=a.a\sqrt{2}.cos45^o=a^2\)
b, \(\left(\overrightarrow{AB}+\overrightarrow{AD}\right)\left(\overrightarrow{BD}+\overrightarrow{BC}\right)=\overrightarrow{AC}\left(\overrightarrow{BD}+\overrightarrow{BC}\right)\)
\(=\overrightarrow{AC}.\overrightarrow{BD}+\overrightarrow{AC}.\overrightarrow{BC}\)
\(=AC.BD.cos90^o+AC.AD.cos45^o\)
\(=a\sqrt{2}.a\sqrt{2}.0+a\sqrt{2}.a.\dfrac{\sqrt{2}}{2}=a^2\)
c, \(\overrightarrow{AB}.\overrightarrow{BD}=AB.BD.cos135^o=-a.a\sqrt{2}.\dfrac{\sqrt{2}}{2}=-a^2\)
d, \(\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\left(2\overrightarrow{AD}-\overrightarrow{AB}\right)=\overrightarrow{BC}.\left(\overrightarrow{AD}+\overrightarrow{BD}\right)\)
\(=\overrightarrow{BC}.\overrightarrow{AD}+\overrightarrow{BC}.\overrightarrow{BD}\)
\(=AD^2+BC.BD.cos45^o\)
\(=a^2+a.a\sqrt{2}.\dfrac{\sqrt{2}}{2}=2a^2\)
e, \(\left(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}\right)\left(\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{DC}\right)\)
\(=\left(\overrightarrow{AC}+\overrightarrow{AC}\right)\left(\overrightarrow{DB}+\overrightarrow{DB}\right)\)
\(=4.\overrightarrow{AC}.\overrightarrow{DB}=4.AC.DB.cos90^o=0\)
Đúng 3
Bình luận (0)
Cho hình vuông ABCD có cạnh là 10, M là trung điểm của BC.
a) Tính giá trị của | vectơ AB+ vectơ AD| và vectơ DM. vectơ DA
b)Tìm tập hợp điểm P thỏa mãn vectơ PA.vectơ BC=10
Cho hình thang ABCD
(
A
B
/
/
C
D
)
c
ó
A
B
A
D
C
D
/
2
.
Gọi M là trung điểm của CD và H là giao điểm của AM và BD.a) Chứng minh tứ giác ABMD là hình thoib) Chứng minh BD ⊥ BCc) Chứng minh ΔAHD và ΔCBD đồng dạngd) Biết A...
Đọc tiếp
Cho hình thang ABCD ( A B / / C D ) c ó A B = A D = C D / 2 . Gọi M là trung điểm của CD và H là giao điểm của AM và BD.
a) Chứng minh tứ giác ABMD là hình thoi
b) Chứng minh BD ⊥ BC
c) Chứng minh ΔAHD và ΔCBD đồng dạng
d) Biết AB = 2,5cm; BD = 4cm. Tính độ dài cạnh BC và diện tích hình thang ABCD.

a) Ta có: AB = AD = CD/2 và M là trung điểm của CD (gt)
⇔ AB = DM và AB // DM
Do đó tứ giác ABMD là hình bình hành có AB = AD. Vậy ABMD là hình thoi.
b) M là trung điểm của CD nên BM là trung tuyến của ΔBDC mà MB = MD = MC. Do đó ΔBDC là tam giác vuông tại B hay DB ⊥ BC
c) ABMD là hình thoi (cmt) ⇔ ∠D1 = ∠D2
Do đó hai tam giác vuông AHD và CBD đồng dạng (g.g)
d) Ta có :
![]()
Xét tam giác vuông AHB, ta có :

Dễ thấy tứ giác ABCM là hình bình hành (AB // CM và AB = CM)
⇒ BC = AM = 3 (cm)
Ta có:
![]()
M là trung điểm của DC nên
SBMD = SBMC = SBCD/2 = 3 (cm2) (chung đường cao kẻ từ B và MD = MC)
Mặt khác ΔABD = ΔMDB (ABCD là hình thoi)
⇔ SABD = SBMD = 3 (cm2)
Vậy SABCD = SABD + SBMD + SBMC = 9 (cm2)
Đúng 1
Bình luận (0)
Cho tứ diện ABCD có BCD là tam giác đều cạnh 1, AB 2. Xét M là điểm thay đổi trên cạnh BC. Mặt phẳng
α
qua M song song với AB và CD lần lượt cắt các cạnh BD, AD, AC tại N, P, Q. Giá trị nhỏ nhất của biểu thức
S
M
P
2
+
N
Q
2
bằng
Đọc tiếp
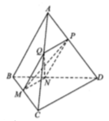
Cho tứ diện ABCD có BCD là tam giác đều cạnh 1, AB = 2. Xét M là điểm thay đổi trên cạnh BC. Mặt phẳng α qua M song song với AB và CD lần lượt cắt các cạnh BD, AD, AC tại N, P, Q. Giá trị nhỏ nhất của biểu thức S = M P 2 + N Q 2 bằng
![]()
![]()
![]()
Cho hình thang ABCD (AB // CD) có AB = AD = CD/2. Gọi M là trung điểm của CD và H là giao điểm của AM và BD. a) Chứng minh tứ giác ABMD là hình thoi b) Chứng minh BD ⊥ BC c) Chứng minh ΔAHD và ΔCBD đồng dạng d) Biết AB = 2,5cm; BD = 4cm. Tính độ dài cạnh BC và diện tích hình thang ABCD.
a ) Ta có : \(AB=AD=\frac{CD}{2}\) và M là trung điểm của CD (gt)
\(\Leftrightarrow AB=DM\) và AB // DM
Do đó tứ giác ABMD là hình bình hành có AB = AD. Vậy ABMD là hình thoi.
b) M là trung điểm của CD nên BM là trung tuyến của \(\Delta BDC\) mà MB = MD = MC.
Do đó \(\Delta BDC\) là tam giác vuông tại B hay \(DB\perp BC\)
c) ABMD là hình thoi (cmt) \(\Leftrightarrow\widehat{D}_1=\widehat{D}_2\)
Do đó hai tam giác vuông AHD và CBD đồng dạng (g.g)
d) Ta có :
\(HB=HD=\frac{1}{2}BD=\frac{1}{2}.4=2\left(cm\right)\)
Xét tam giác vuông AHB, ta có :
\(AH=\sqrt{AB^2-HB^2}\) ( định lí Pitago )
\(=\sqrt{2,5^2-2^2}=1,5\left(cm\right)\)
\(\Rightarrow AM=3\left(cm\right)\)
Dễ thấy tứ giác ABCM là hình bình hành (AB // CM và AB = CM)
\(\Rightarrow BC=AM=3\left(cm\right)\)
Ta có :
\(S_{BDC}=\frac{1}{2}BD.BC=\frac{1}{2}.4.3=6\left(cm^2\right)\)
M là trung điểm của DC nên
\(S_{BMD}=S_{BMC}=\frac{S_{BCD}}{2}=3\left(cm^2\right)\)
(chung đường cao kẻ từ B và MD = MC)
Mặt khác \(\Delta ABD=\Delta MDB\) ( ABCD là hình thoi )
\(\Leftrightarrow S_{ABD}=S_{BMD}=3\left(cm^2\right)\)
Vậy \(S_{ABCD}=S_{ABD}+S_{BMD}+S_{BMC}=9\left(cm^2\right)\)
Chúc bạn học tốt !!!
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có BCD là tam giác đều cạnh 1, AB 2. Xét M là điểm thay đổi trên canh BC. Mặt phẳng (α) qua M song song với AB và CD lần lượt cắt các cạnh BD, AD, AC tại N, P, Q. Giá trị nhỏ nhất của biểu thức
S
M
P
2
+
N
Q
2
bằng A.
8
5
B.
34
9
C.
3
4...
Đọc tiếp
Cho tứ diện ABCD có BCD là tam giác đều cạnh 1, AB = 2. Xét M là điểm thay đổi trên canh BC. Mặt phẳng (α) qua M song song với AB và CD lần lượt cắt các cạnh BD, AD, AC tại N, P, Q. Giá trị nhỏ nhất của biểu thức S = M P 2 + N Q 2 bằng
A. 8 5
B. 34 9
C. 3 4
D. 8 9
1. Cho tam giác ABC vuông tại A, AB = 5, AC = 7. Tính giá trị của \(\overrightarrow{AB}\).\(\overrightarrow{BC}\)?
2. Cho hình chữ nhật ABCD, AB = 8, AD = 5. Tính giá trị của \(\overrightarrow{AB}\).\(\overrightarrow{BD}\)?
1.
\(\overrightarrow{AB}.\overrightarrow{BC}=\overrightarrow{AB}.\left(\overrightarrow{BA}+\overrightarrow{AC}\right)=\overrightarrow{AB}.\left(-\overrightarrow{AB}\right)+\overrightarrow{AB}.\overrightarrow{AC}=-AB^2=-25\)
2.
\(\overrightarrow{AB}.\overrightarrow{BD}=\overrightarrow{AB}\left(\overrightarrow{BA}+\overrightarrow{AD}\right)=-\overrightarrow{AB}.\overrightarrow{AB}+\overrightarrow{AB}.\overrightarrow{AD}=-AB^2+0=-64\)
Đúng 1
Bình luận (0)
1. Cho tam giác ABC vuông tại A, ABAC. AH vuông góc với BC. Trên AC lấy điểm D sao cho ADAB. M là trung điểm của BD. Chứng minh HM là tia phân giác của góc AHC.2. Cho hình chữ nhật ABCD. TRên các cạnh AB, AC, CD, DA lấy lần lượt các điểm M, N, P, Q. Tìm giá trị nhỏ nhất của chu vi tứ giác MNPQ.3. Cho hình chữ nhật ABCD có AB 3, BC6. Trong hình chữ nhật lấy 10 điểm. Chứng minh rằng tồn tại ít nhất 2 điểm có khoảng cách nhỏ hơn 2,3.Các bạn giúp mình với nhé. Cảm ơn.
Đọc tiếp
1. Cho tam giác ABC vuông tại A, AB<AC. AH vuông góc với BC. Trên AC lấy điểm D sao cho AD=AB. M là trung điểm của BD. Chứng minh HM là tia phân giác của góc AHC.
2. Cho hình chữ nhật ABCD. TRên các cạnh AB, AC, CD, DA lấy lần lượt các điểm M, N, P, Q. Tìm giá trị nhỏ nhất của chu vi tứ giác MNPQ.
3. Cho hình chữ nhật ABCD có AB= 3, BC=6. Trong hình chữ nhật lấy 10 điểm. Chứng minh rằng tồn tại ít nhất 2 điểm có khoảng cách nhỏ hơn 2,3.
Các bạn giúp mình với nhé. Cảm ơn.