Chứng minh rằng:3 đơn thức-1phần 2xy2 ;-3phần 4x3y;2y không thể cùng có giá trị âm
Những câu hỏi liên quan
Cho B = 1phần 2 +(1phần 2 mũ 2)+(1phần 2 mũ 3) +.......+(1phần 2mũ 98) +(1phần 2 mũ 99)
Chứng minh rằng B<1
\(B=\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{98}}+\dfrac{1}{2^{99}}\\ =\left(2-1\right)\cdot\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{98}}+\dfrac{1}{2^{99}}\right)\\ =1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{2^2}+\dfrac{1}{2^2}-\dfrac{1}{2^3}+...+\dfrac{1}{2^{98}}-\dfrac{1}{2^{99}}\\ =1-\dfrac{1}{2^{99}}< 1\)
Vậy \(B< 1\)
Đúng 0
Bình luận (0)
\(B=\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{98}}+\dfrac{1}{2^{99}}\)
\(\Rightarrow2B=2\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{98}}+\dfrac{1}{2^{99}}\right)\)
\(\Rightarrow2B=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{97}}+\dfrac{1}{2^{98}}\)
\(\Rightarrow2B-B=\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{97}}+\dfrac{1}{2^{98}}\right)-\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{98}}+\dfrac{1}{2^{99}}\right)\)
\(\Rightarrow B=1-\dfrac{1}{2^{99}}\)
\(\rightarrow B< 1\rightarrowđpcm\)
Đúng 0
Bình luận (0)
Chứng minh đẳng thức sau:
x
2
y
+
2
x
y
2
+
y
3
2
x
2
+
x
y
-
y
2
x...
Đọc tiếp
Chứng minh đẳng thức sau: x 2 y + 2 x y 2 + y 3 2 x 2 + x y - y 2 = x y + y 2 2 x - y
Chứng minh đẳng thức:
2x2+3xy+y2/2x3+x2y-2xy2-y3=1/x-y
\(VT=\dfrac{2x^2+2xy+xy+y^2}{x^2\left(2x+y\right)-y^2\left(2x+y\right)}=\dfrac{2x\left(x+y\right)+y\left(x+y\right)}{\left(x^2-y^2\right)\left(2x+y\right)}\\ =\dfrac{\left(2x+y\right)\left(x+y\right)}{\left(2x+y\right)\left(x-y\right)\left(x+y\right)}=\dfrac{1}{x-y}=VP\)
Đúng 2
Bình luận (0)
Chứng minh các đẳng thức sau:
x
2
y
+
2
x
y
2
+
y
3
2
x
2
+
x
y
-...
Đọc tiếp
Chứng minh các đẳng thức sau: x 2 y + 2 x y 2 + y 3 2 x 2 + x y - y 2 = x y + y 2 2 x - y
Ta có
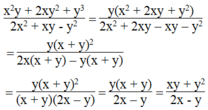
Vế trái bằng vế phải nên đẳng thức được chứng minh.
Đúng 0
Bình luận (0)
Bài 6A: (Tăng cường – Trang 43)
Cho đơn thức A 2xy2 (1/2x2 y2 x)
a)Thu gọn đơn thức A
b)Tìm bậc của đơn thức thu gọn
c)Xác định phần hệ số, phần biến của đơn thức thu gọn
d)Tính giá trị của đơn thức tại x 1, y -1
e)Chứng minh rằng A luôn nhận giá trị dương với mọi x ≠0 và y ≠ 0.
Bài 6B: (Tăng cường – Trang 43)
Cho đơn thức A 2/3xy2 (3/2x)
a)Thu gọn đơn thức A
b)Tìm bậc của đơn thức thu gọn
c)Tính giá trị của đơn thức thu gọn.
d)Tính giá trị của đơn thức tại x 1, y 2
e)Chứn...
Đọc tiếp
Bài 6A: (Tăng cường – Trang 43)
Cho đơn thức A = 2xy2 (1/2x2 y2 x)
a)Thu gọn đơn thức A
b)Tìm bậc của đơn thức thu gọn
c)Xác định phần hệ số, phần biến của đơn thức thu gọn
d)Tính giá trị của đơn thức tại x = 1, y = -1
e)Chứng minh rằng A luôn nhận giá trị dương với mọi x ≠0 và y ≠ 0.
Bài 6B: (Tăng cường – Trang 43)
Cho đơn thức A = 2/3xy2 (3/2x)
a)Thu gọn đơn thức A
b)Tìm bậc của đơn thức thu gọn
c)Tính giá trị của đơn thức thu gọn.
d)Tính giá trị của đơn thức tại x = 1, y = 2
e)Chứng minh rằng A luôn nhận giá trị dương với mọi x≠0
và y ≠ 0.
Bài 13: (Tăng cường – Trang 44)
Cho đơn thức A=-3/8x2 y2 . 2/3xy2 z2 . 4/5x3 y
a)Thu gọn đơn thức
b)Tìm bậc của đơn thức
c)Tính giá trị của đơn thức tại x=-1, y =-2, z=3.
d)Đơn thức A có thể nhận giá trị dương được không?
Chứng minh đẳng thức:
2
x
2
+
3
xy
+
y
2
2
x
3
+
x
2
y
−
2
xy...
Đọc tiếp
Chứng minh đẳng thức: 2 x 2 + 3 xy + y 2 2 x 3 + x 2 y − 2 xy 2 − y 3 = 1 x − y với y ≠ − 2 x và y ≠ ± x .
Cho đơn thức M = ( - 1 2 x α y ) , N = ( - 2 x y 2 ) . Tìm a để bậc của đơn thức P = M.N là 9
A. 4
B. 5
C. 6
D. 7
Chọn C
Ta có: P = M.N = (-1/2 xay)(-2xy2) = x(a + 1) y3.
Khi đó bậc của đơn thức là a + 1 + 2 = a + 3
Vì bậc của đơn thức là 9 nên a + 3 = 9 ⇒ a = 6.
Đúng 0
Bình luận (0)
1. Thu gọn rồi tìm bậc của các đơn thức a A −2x2y3z .14 xy.5x3b B 3x2y 2xy2−13 x2y 3xy2 43 x2y−2xy2
Có số mũ chứ.
a, A=-2x^2.y^3.z.14xy.5x^3
= (-2.14.5).(x^2.x.x^3).(y^3.y)
= -140.x^6.y^4. Bậc : 10
b, B= 3x^2.y.2xy^2.(-13x^2.y).3xy^2.43x^2.y.(-2xy^2)
= [(-13).(-2).3.2.3.43].(x^2.x.x^2.x.x^2.x).(y.y^2.y.y^2.y.y^2)
= 20124.x^9.y^9. Bậc: 18
Đáp án kiểu j ấy. Chắc sai.
Xếp các đơn thức sau thành từng nhóm các đơn thức đồng dạng:
5
3
x
2
y
;
x
y
2
;
-
1
2
x
2
y
;
-
2
x
y
2
;
x
2
y
;...
Đọc tiếp
Xếp các đơn thức sau thành từng nhóm các đơn thức đồng dạng: 5 3 x 2 y ; x y 2 ; - 1 2 x 2 y ; - 2 x y 2 ; x 2 y ; 1 4 x y 2 ; - 2 5 x 2 y ; x y
Các nhóm đơn thức đồng dạng là:
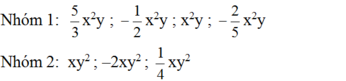
Vì nhóm 1 có phần biến chung là: x2y, nhóm 2 có phần biến chung là: xy2
Còn lại đơn thức xy (có phần biến là xy) không đồng dạng với các đơn thức nào đã cho.
Đúng 0
Bình luận (0)